题目描述
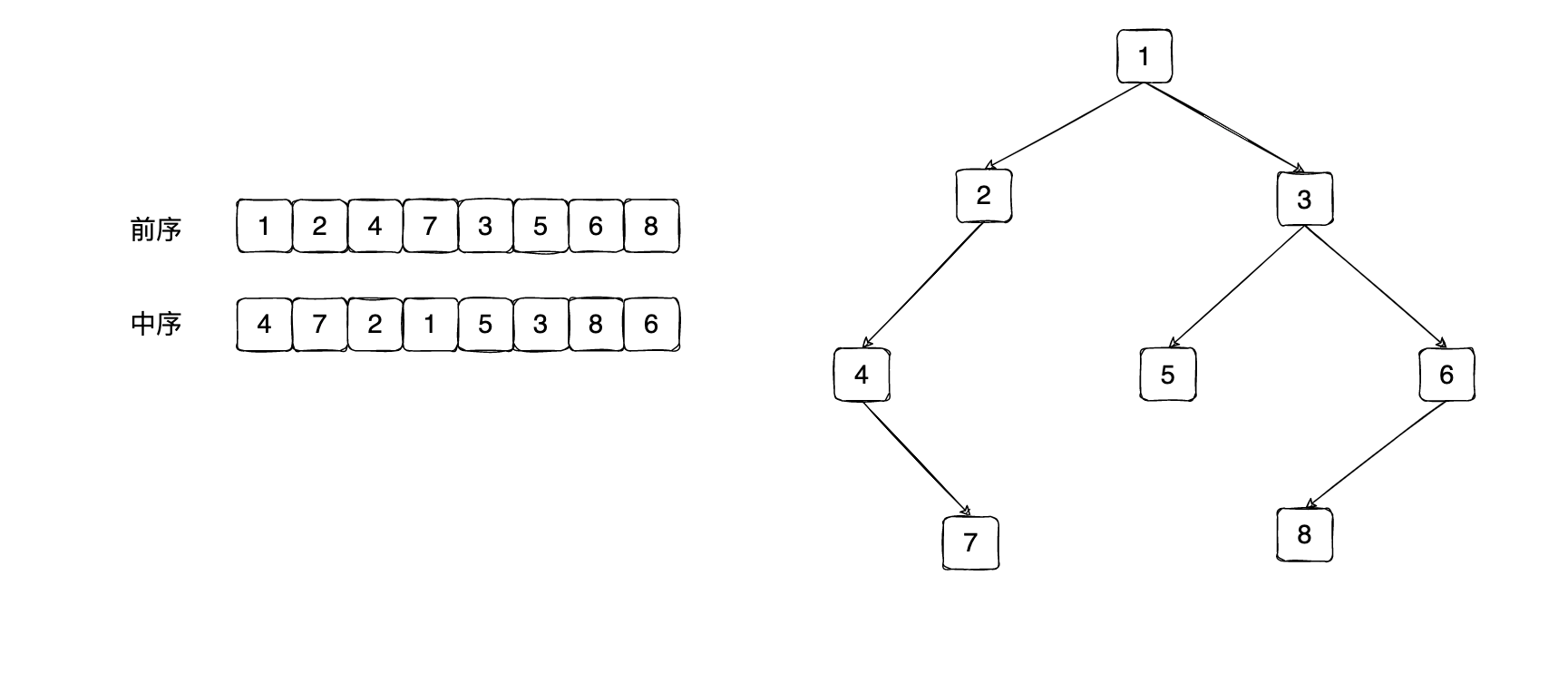
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路 & 解答
递归解决
我们看上面的图片,首先数据保证了正确性,那么前序的第一个肯定是root节点,也就是1,那么我们需要在中序遍历中找到1的位置,左边就是这个root的左子树,右边就是root的右子树。
我们可以举个栗子:对根节点的左子树进行解析:
对右子树进行解析:
只需要不断递归即可,当边界左边大于右边的时候,则停止。
Java 代码如下:
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
if (pre == null || pre.length == 0 || in == null || in.length == 0) {
return null;
}
TreeNode root = constructBinaryTree(pre, 0, pre.length - 1, in, 0, in.length-1);
return root;
}
TreeNode constructBinaryTree(int[] pre, int startPre, int endPre, int[] in, int startIn, int endIn) {
// 不符合条件直接返回null
if (startPre > endPre || startIn > endIn) {
return null;
}
// 构建根节点
TreeNode root = new TreeNode(pre[startPre]);
for (int index = startIn; index <= endIn; index++) {
if (in[index] == pre[startPre]) {
// 左子树
root.left = constructBinaryTree(pre, startPre + 1, startPre + (index - startIn), in, startIn, index - 1);
// 右子树
root.right = constructBinaryTree(pre, (index - startIn) + startPre + 1, endPre, in, index + 1, endIn);
break;
}
}
return root;
}
}
C++ 代码如下:
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode *reConstructBinaryTree(vector<int> pre, vector<int> in) {
if (pre.size() == 0 || in.size() == 0) {
return NULL;
}
TreeNode *root = constructBinaryTree(pre, 0, pre.size() - 1, in, 0, in.size() - 1);
return root;
}
TreeNode *constructBinaryTree(vector<int> pre, int startPre, int endPre, vector<int> in, int startIn, int endIn) {
// 不符合条件直接返回null
if (startPre > endPre || startIn > endIn) {
return NULL;
}
// 构建根节点
TreeNode *root = new TreeNode(pre[startPre]);
for (int index = startIn; index <= endIn; index++) {
if (in[index] == pre[startPre]) {
// 左子树
root->left =
constructBinaryTree(pre, startPre + 1, startPre + (index - startIn), in, startIn, index - 1);
// 右子树
root->right =
constructBinaryTree(pre, (index - startIn) + startPre + 1, endPre, in, index + 1, endIn);
break;
}
}
return root;
}
};
栈解法
所有的递归理论上都可以用栈模拟,那么我们如何用栈解答呢?
我们可以一开始创建一个栈,分别用两个指针执行前序遍历和中序遍历的第一个元素,先将前序遍历的第一个元素压入栈中,因为前序遍历的特性,第一个元素肯定是根节点。
- 开始循环,对比栈顶的元素和中序遍历数组的元素
- 1 如果不相等,说明当前栈顶元素还有左子树,因为如果没有左子树的话,前序的第一个元素和中序的第一个元素应该相等。既然有左子树,那么前序遍历指针指向的元素就是它的左子树根节点,建立关系,压栈。
- 2 如果相等,那么说明当前的栈顶元素已经没有左子树了。
- 2.1 把栈顶元素和中序遍历的元素对比,相等则弹出之后,继续对比下一个元素与当前的栈顶元素,直到不相等为止。(相等说明没有右节点,弹出以为着退出上一层)
- 2.2 不相等的时候,需要把当前的元素作为右叶子节点,压入栈中。
上面的文字可能比较难懂,但是不紧要,下面图文说明:
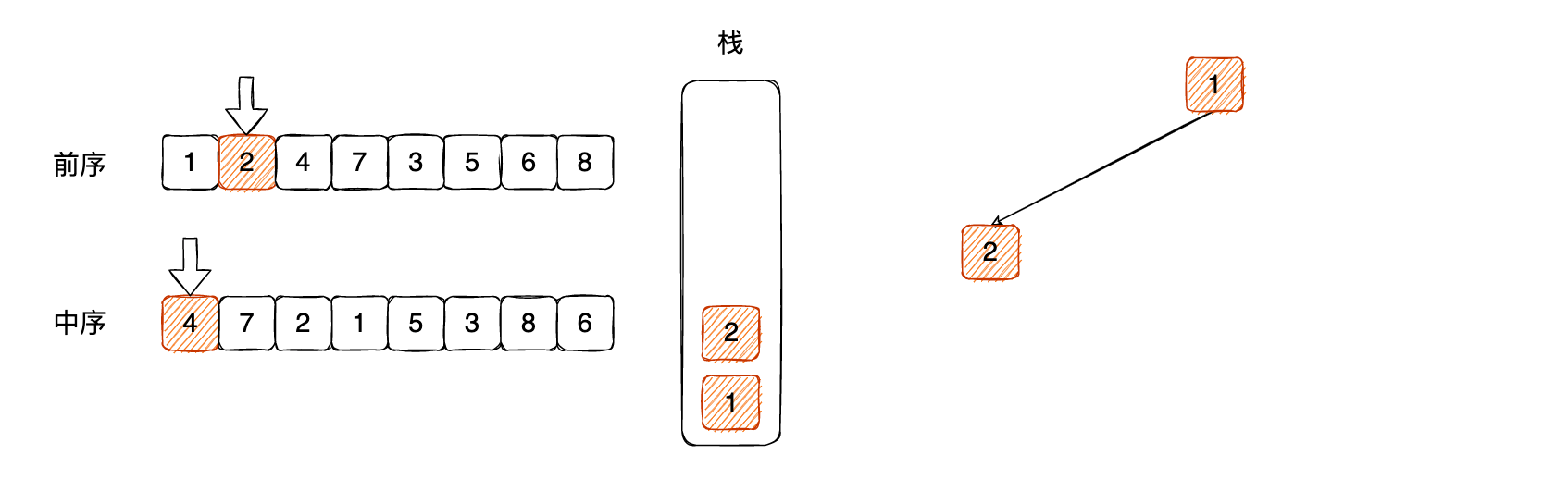
首先我们有前序和中序遍历的数组,原树结构大致了解一下:
把当前的前序遍历的元素 1 先放到栈里面,这个肯定是根节点:

对比中序遍历第一个元素 4,和栈顶元素 1,不相等,那么说明有左子树,前序遍历的第 2 个元素 2 就是左子树节点,关联成左子树,压栈:
同样得不相等,会持续压栈:
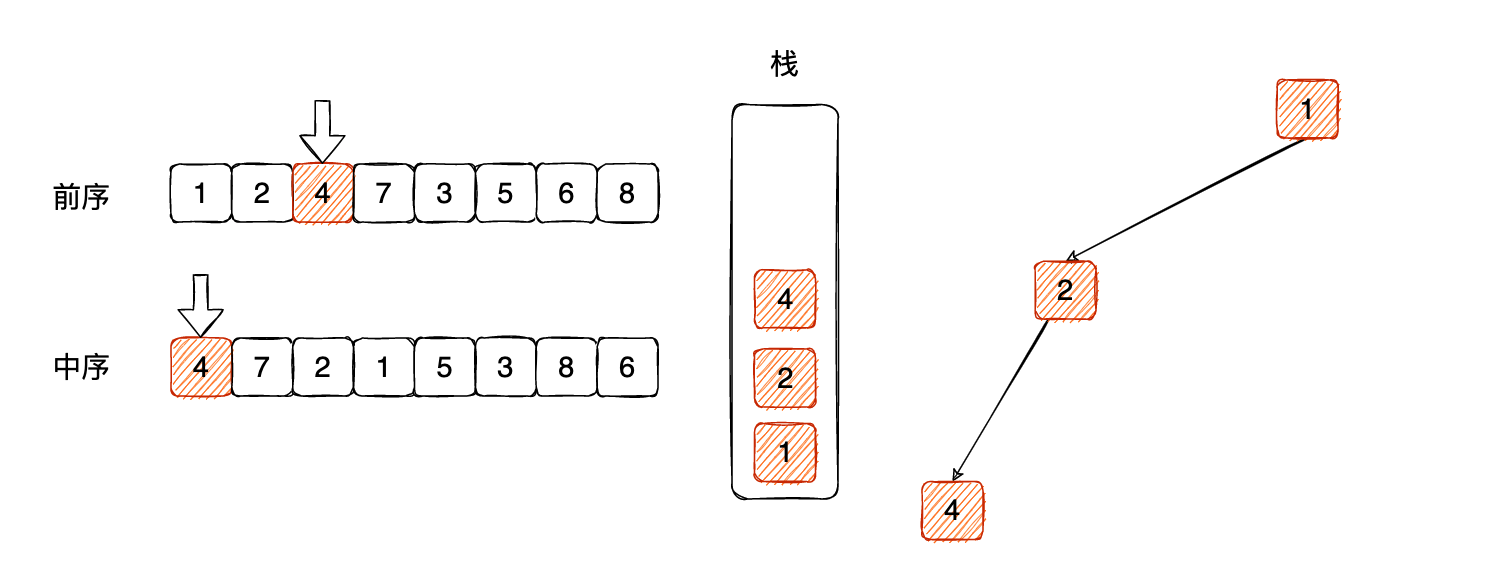

直到,中序遍历的第一个元素 4,已经等于栈顶元素 4,说明4 没有左子树了,因为 4 是在中序遍历里面,中序遍历完根节点,剩下的部分只能是右子树。
那么把 4 弹出去,中序遍历指针移动到下一个位置:
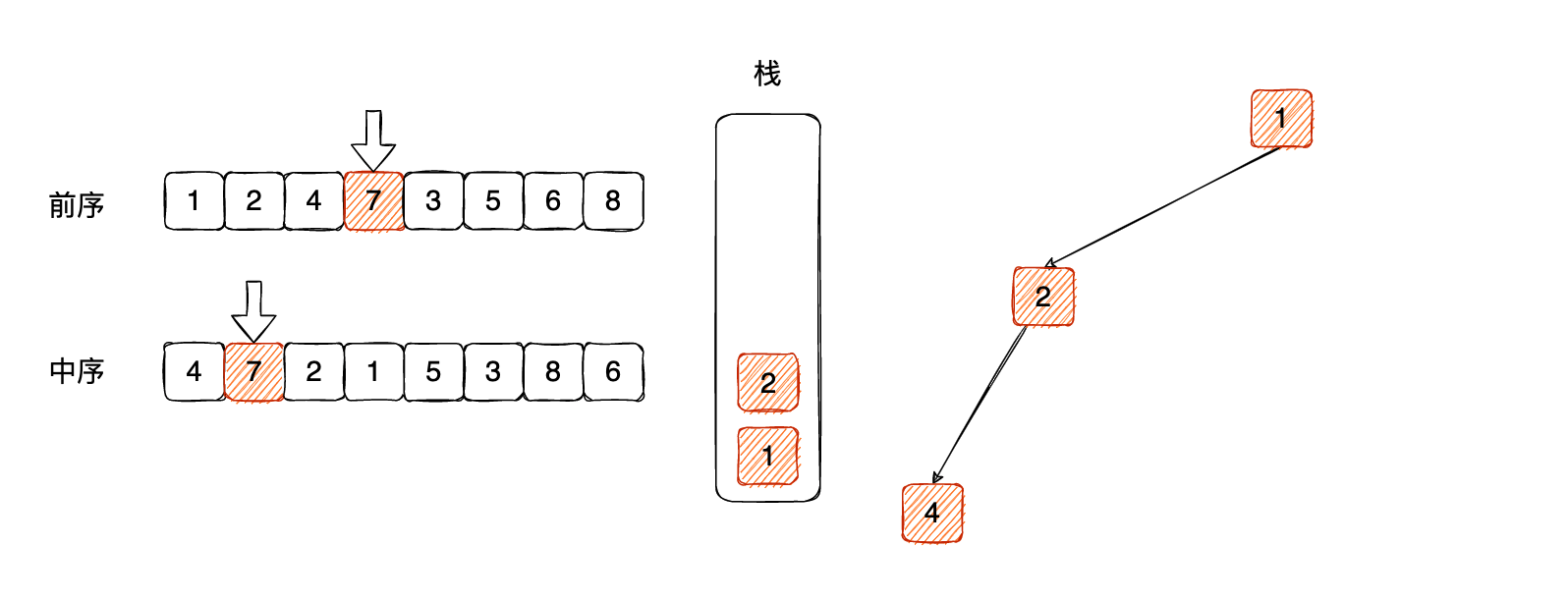
这个时候,7 肯定是之前节点 4 的右子树节点,那么关联关系之后,压入栈里面:

此时,结束了一次循环,注意前序遍历的指针会往后移动一位。
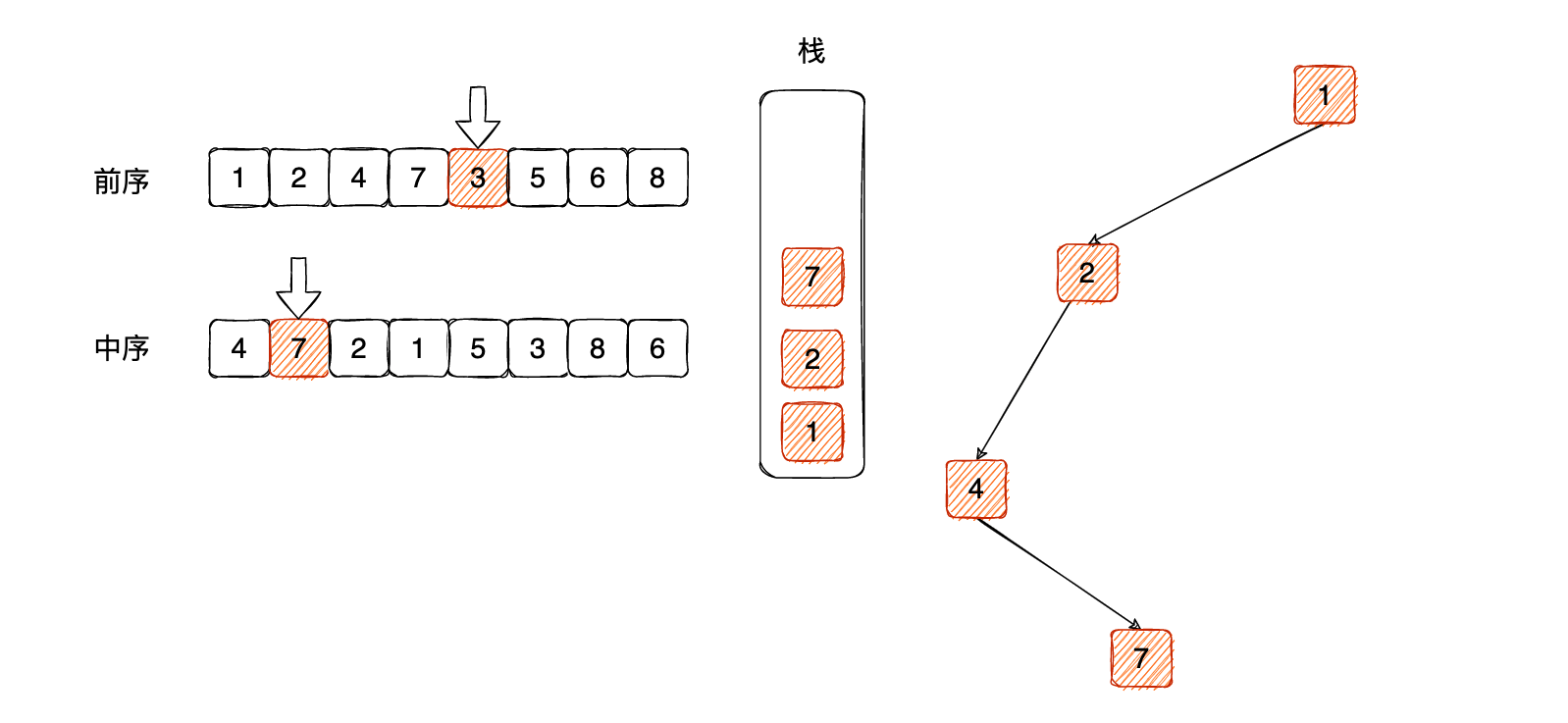
再次循环的时候,依然判断中序遍历中的数值是否等于栈顶元素,发现都是7,相等。弹出,移动到下一个位置,相当于退出了上一层:

依旧 2==2 相等,再次弹出:
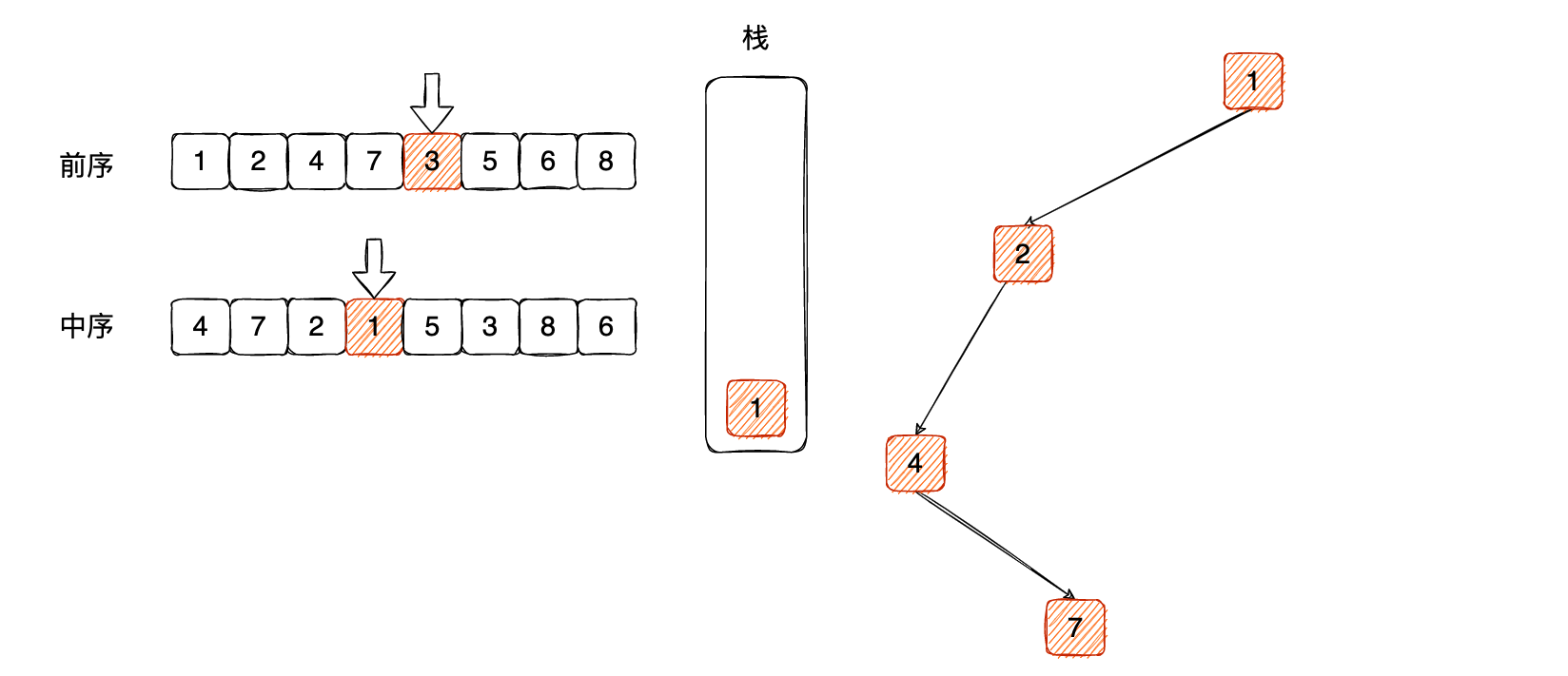
同样中序遍历的 1 还是等于栈顶的 1,弹出,移动到下一位:
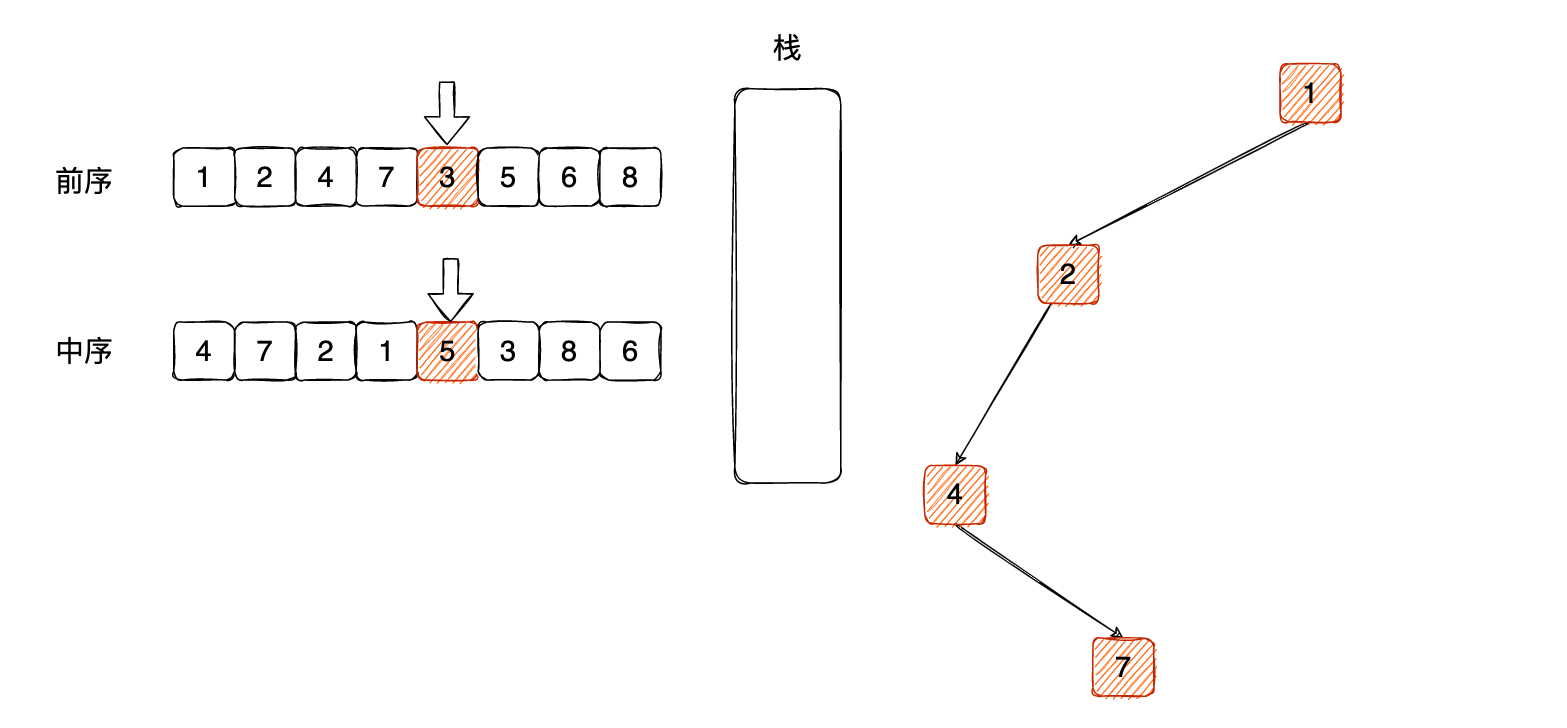
这个时候,栈顶元素的 1 已经被取出来了,说明左子树全部遍历完成了,剩下的部分是它的右子树内容了,那么前序遍历中,3就必定是根节点1的右子树的根,压入栈中,前序遍历索引指向下一个元素:
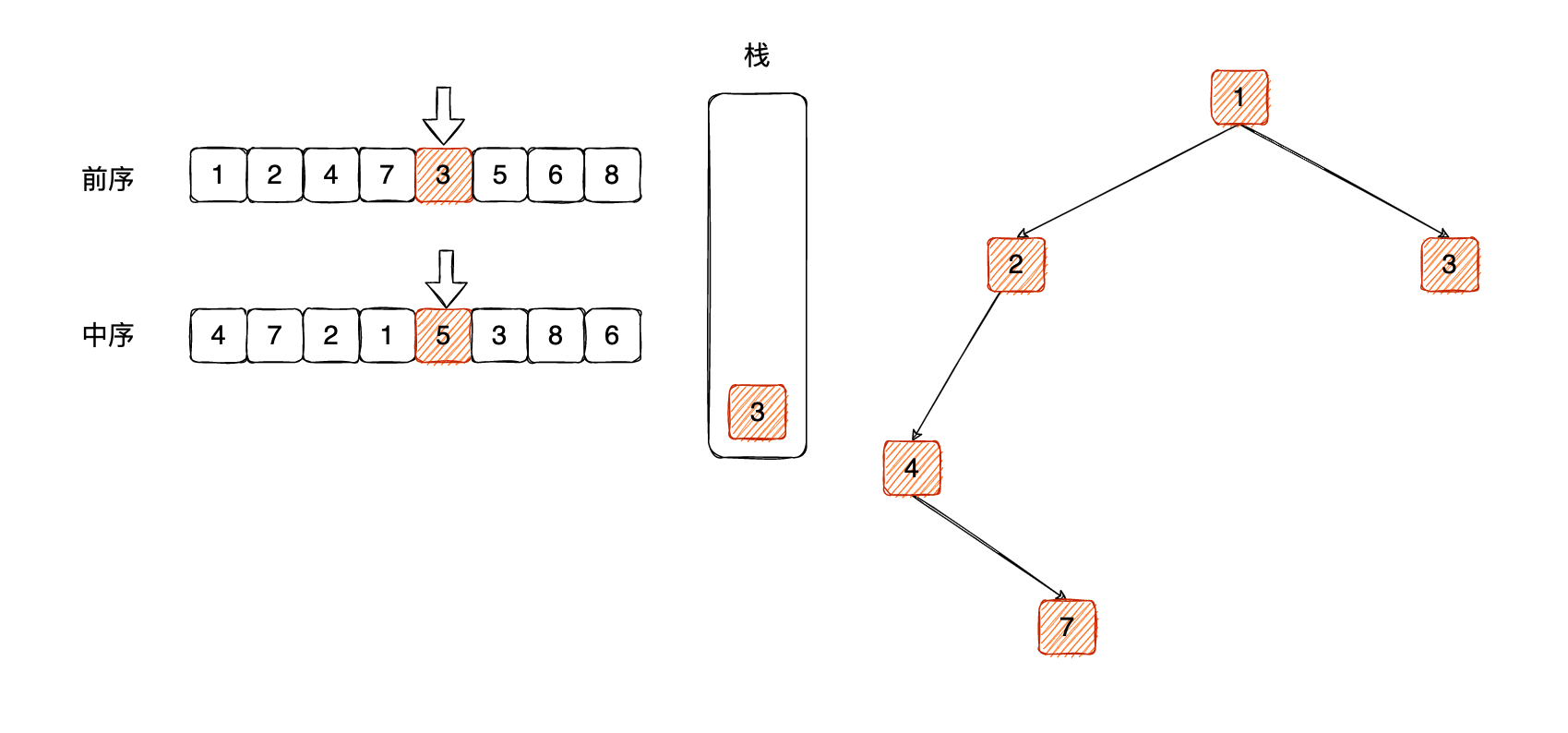
到这里其实是结束了第二轮的循环。
再次循环,判断中序遍历的数值和栈顶元素不相等,那么说明是左子树,前序遍历中的 5 压入栈内,索引后移:


中序遍历的数值和栈顶元素一对比,发现相等,说明5没有左子树了,弹出,索引后移:

依然 两个都是 3(说明 3 的左子树被遍历完成了,剩下的是 3 的右子树了),继续弹出,后移

此时,3 是刚刚弹出的元素,剩下的元素都是它的右子树,那么前序遍历中指向的数组6就是3的右子树,6 压入栈中:
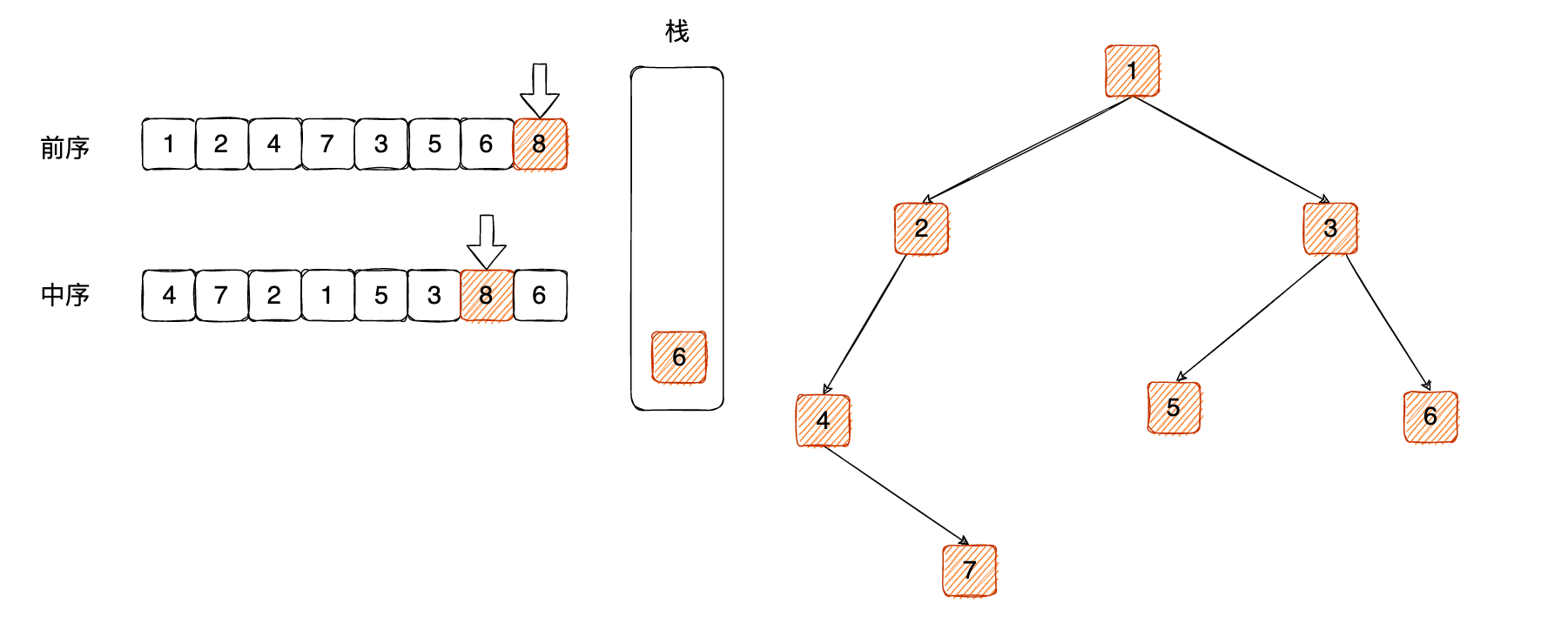
对比栈顶元素6 和中序遍历中的8 发现不相等,那么把前序遍历中的 8 压栈,成为左子树:
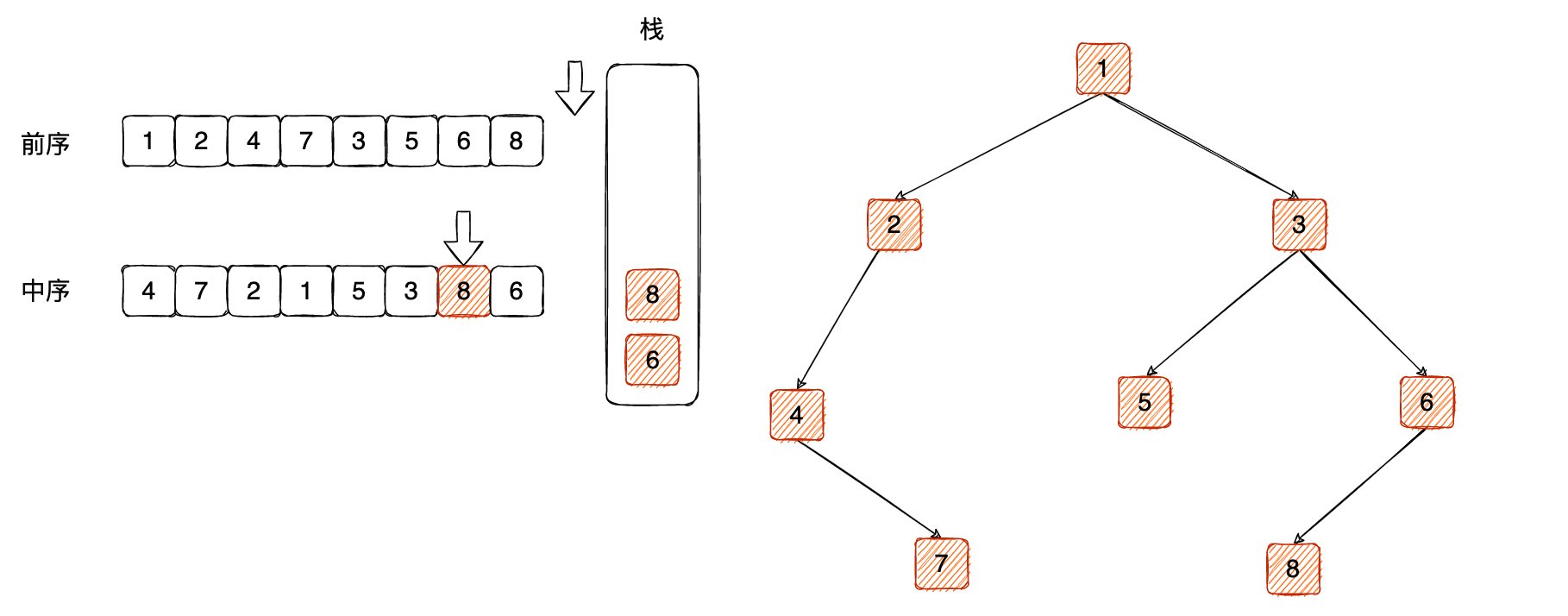
对比栈顶元素 8 和中序遍历的 8 ,相等则弹出:
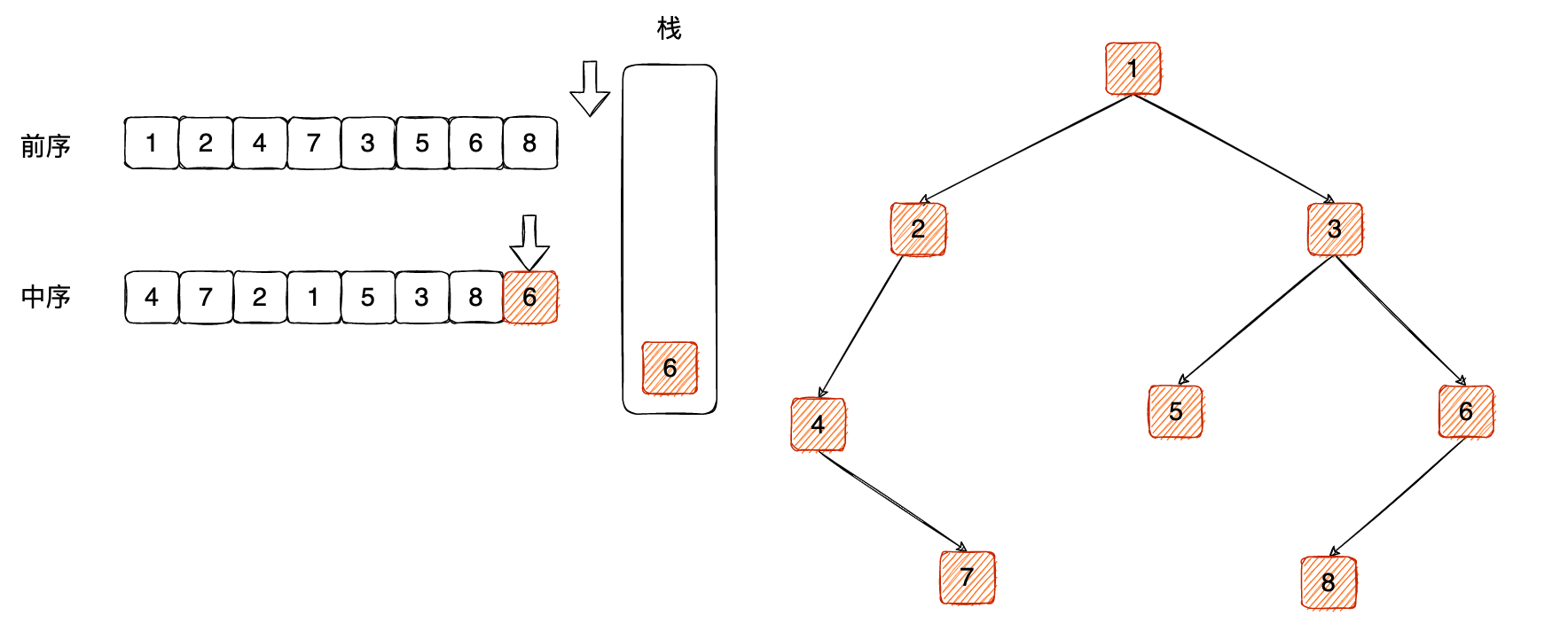
还是相等,继续弹出:
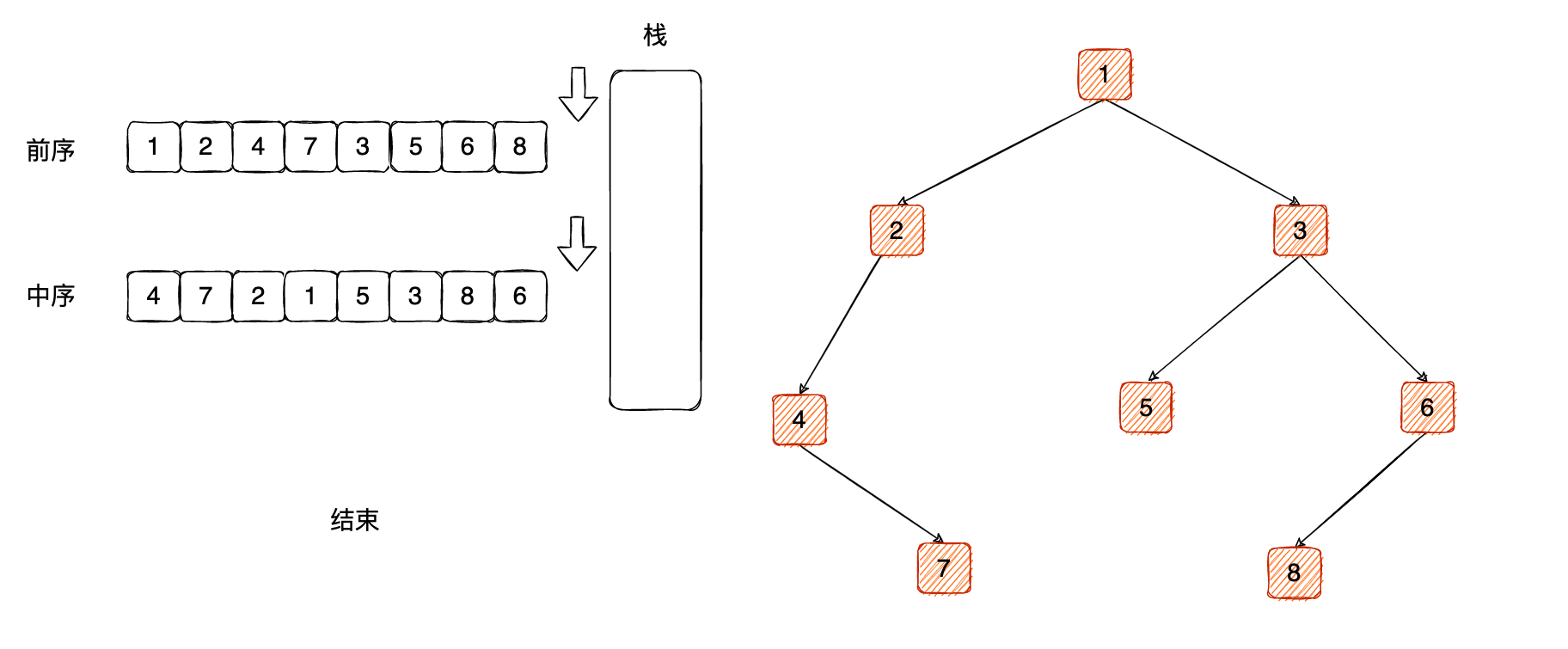
栈里面没有元素,并且数组都遍历结束,整个过程结束。
Java 代码实现如下:
import java.util.Stack;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution7 {
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
// 判空
if (pre == null || pre.length == 0 || in == null || in.length == 0) {
return null;
}
Stack<TreeNode> stack = new Stack<>();
int preIndex = 0;
int inIndex = 0;
TreeNode root = new TreeNode(pre[preIndex]);
stack.push(root);
for (preIndex = 1; preIndex < pre.length; preIndex++) {
TreeNode node = stack.peek();
// 不相等说明还有左子树
if (node.val != in[inIndex]) {
// 关联成为左子树,压栈
node.left = new TreeNode(pre[preIndex]);
stack.push(node.left);
} else {
// 相等说明,当前节点没有左子树
while (!stack.isEmpty() && stack.peek().val == in[inIndex]) {
// 只要两者相等,说明没有右子树,弹出节点,退到上一层
node = stack.pop();
inIndex++;
}
// 有右子树,关联
node.right = new TreeNode(pre[preIndex]);
stack.push(node.right);
}
}
return root;
}
}
C++ 代码如下:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
TreeNode *reConstructBinaryTree(vector<int> pre, vector<int> vin) {
// 判空
if (pre.size() == 0 || vin.size() == 0) {
return NULL;
}
stack<TreeNode *> stack;
int preIndex = 0;
int inIndex = 0;
TreeNode *root = new TreeNode(pre[preIndex]);
stack.push(root);
for (preIndex = 1; preIndex < pre.size(); preIndex++) {
TreeNode *node = stack.top();
// 不相等说明还有左子树
if (node->val != vin[inIndex]) {
// 关联成为左子树,压栈
node->left = new TreeNode(pre[preIndex]);
stack.push(node->left);
} else {
// 相等说明,当前节点没有左子树
while (stack.size() != 0 && stack.top()->val == vin[inIndex]) {
// 只要两者相等,说明没有右子树,弹出节点,退到上一层
node = stack.top();
stack.pop();
inIndex++;
}
// 有右子树,关联
node->right = new TreeNode(pre[preIndex]);
stack.push(node->right);
}
}
return root;
}
};
