题目描述

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

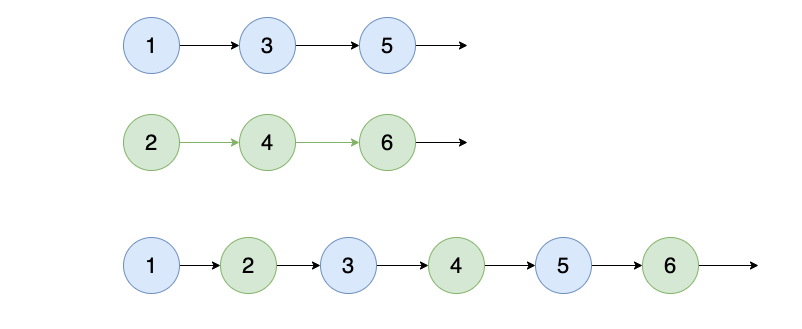
如输入{1,3,5},{2,4,6}时，合并后的链表为{1,2,3,4,5,6}，所以对应的输出为{1,2,3,4,5,6}，转换过程如下图所示：

思路 & 解答

思路比较清晰，首先创建一个 -1 节点的新链表，然后两个链表都从头开始，循环到直到一个链表遍历到最后，谁的节点小，就加入新的链表后面。然后遍历两个链表剩下的元素，这些元素肯定比另一个链表的所有元素都大或者相等，直接加入新的链表后面即可。

代码如下：

    public ListNode Merge(ListNode list1,ListNode list2) {
        if(list1==null){
            return list2;
        }else if(list2==null){
            return list1;
        }else{
            ListNode head = new ListNode(-1);
            ListNode first = head;
            while(list1!=null&&list2!=null){
                if(list1.val<list2.val){
                    first.next = new ListNode(list1.val);
                    list1=list1.next;
                }else {
                    first.next = new ListNode(list2.val);
                    list2 = list2.next;
                }
                first = first.next;
            }
            while(list1!=null){
                first.next = new ListNode(list1.val);
                list1=list1.next;
                first = first.next;
            }
            while(list2!=null){
                first.next = new ListNode(list2.val);
                list2=list2.next;
                first = first.next;
            }
            return head.next;
        }
    }

C++ 代码实现如下：

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode *Merge(ListNode *list1, ListNode *list2) {
        if (list1 == NULL) {
            return list2;
        } else if (list2 == NULL) {
            return list1;
        } else {
            ListNode *head = new ListNode(-1);
            ListNode *first = head;
            while (list1 != NULL && list2 != NULL) {
                if (list1->val < list2->val) {
                    first->next = new ListNode(list1->val);
                    list1 = list1->next;
                } else {
                    first->next = new ListNode(list2->val);
                    list2 = list2->next;
                }
                first = first->next;
            }
            while (list1 != NULL) {
                first->next = new ListNode(list1->val);
                list1 = list1->next;
                first = first->next;
            }
            while (list2 != NULL) {
                first->next = new ListNode(list2->val);
                list2 = list2->next;
                first = first->next;
            }
            return head->next;
        }
    }
};

时间复杂度：O(m+n),m，n分别为两个单链表的长度 空间复杂度：O(1)

其实这道题还有一个迭代版本，那就是取当前两个链表的更小值，然后递归剩下的链表之间的比较，直到一个为空。

Java 代码如下：

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {
        if (list1==null) return list2;
        if (list2==null) return list1;
        if (list1.val <= list2.val) {
            list1.next = Merge(list1.next, list2);
            return list1;
        }
        else {
            list2.next = Merge(list1, list2.next);
            return list2;
        }
    }
}

C++ 代码如下：

#include<stdio.h>

struct ListNode {
    int val;
    struct ListNode *next;

    ListNode(int x) :
            val(x), next(NULL) {
    }
};

class Solution {
public:
    ListNode* Merge(ListNode* list1, ListNode* list2)
    {
        if (!list1) return list2;
        if (!list2) return list1;
        if (list1->val <= list2->val) {
            list1->next = Merge(list1->next, list2);
            return list1;
        }
        else {
            list2->next = Merge(list1, list2->next);
            return list2;
        }
    }
};

时间复杂度：O(m+n) 空间复杂度：O(m+n),递归其实需要消耗栈，递归一次需要存储至少一个变量。