题目描述

给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。 窗口大于数组长度的时候，返回空。

示例1

输入

[2,3,4,2,6,2,5,1],3

返回值

[4,4,6,6,6,5]

思路 & 解答

首先进行非空判断，以及数组长度是否不为0，是否不小于窗口长度。

其次，使用一个双向链表，里面保存的是索引，遍历每一个元素，如果双向队列不为空且最后的元素作为索引的数值小于当前的元素，就把当前的元素的索引加到队列的后面。（这样可以保证队列从头到尾是单调递减少的，也就是队尾的元素就是最小的元素）。

然后把当前的元素加进去队列尾部。判断队列前面的元素是不是索引位置不符合，如果不符合，就移除队列头部的元素。

那么此时的队列首部肯定就是滑动窗口的最大值。（此处应该判断滑动窗口生效的索引）

以2, 3, 4, 2, 6, 2, 5, 1为例：

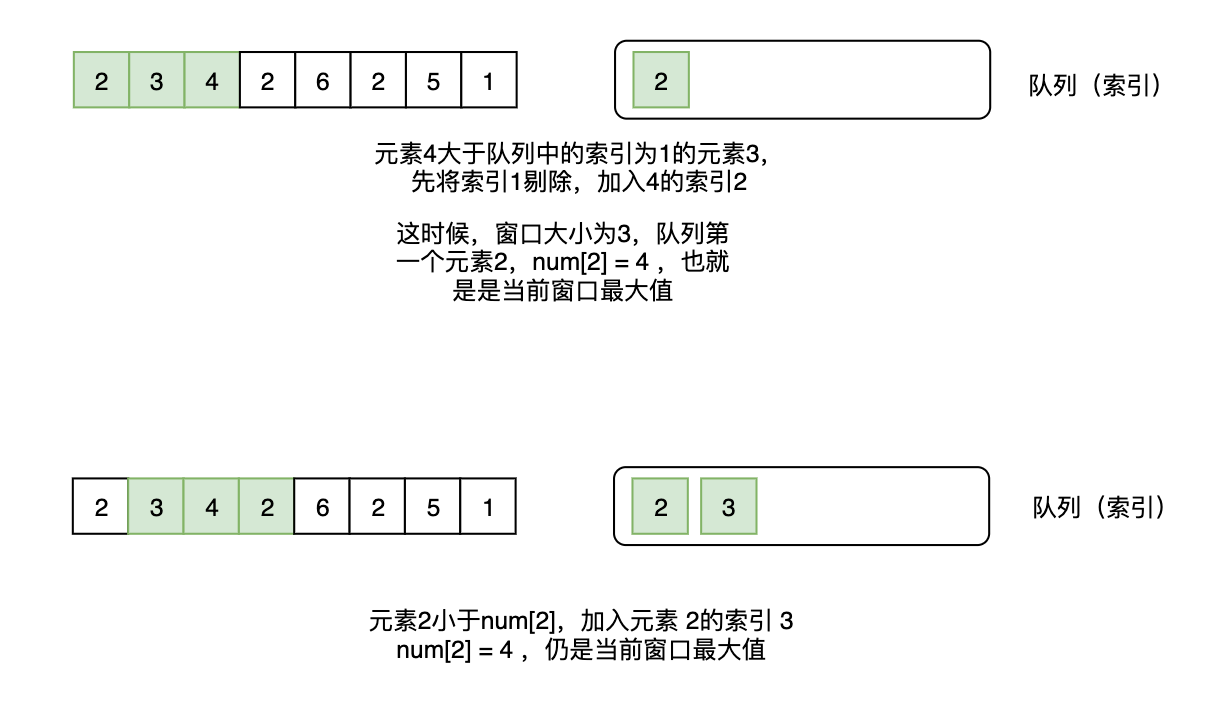
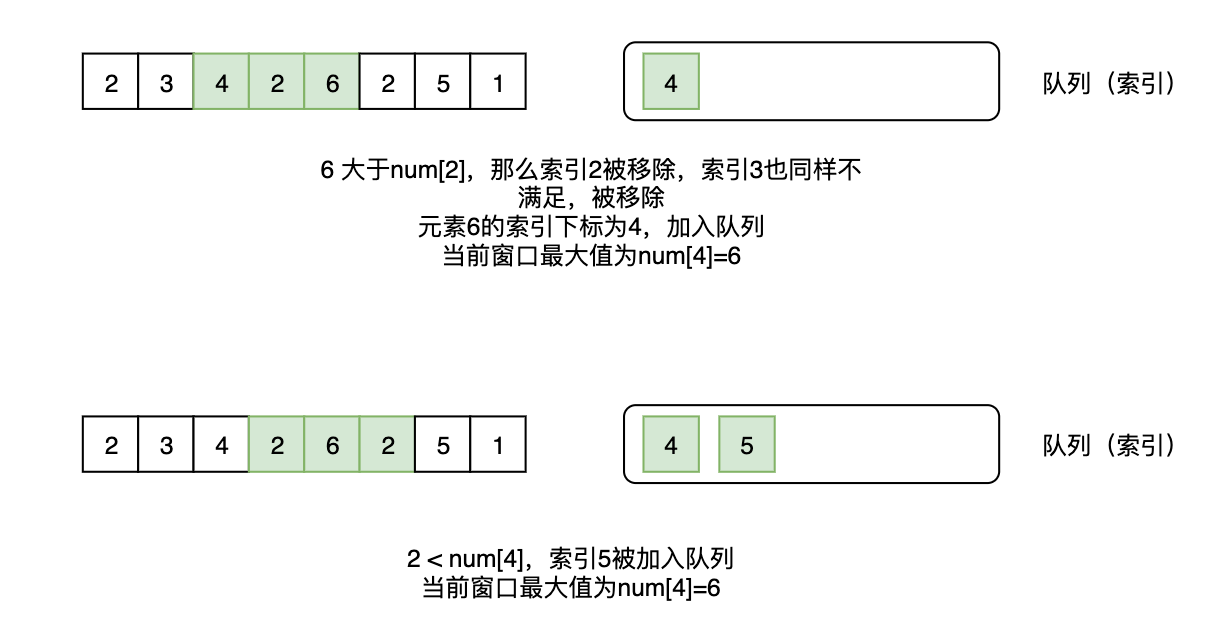
所有的窗口最大值至此已经收集完成。

import java.util.*;

public class Solution64 {
    public static void main(String[] args) {
        int[] nums = {2, 3, 4, 2, 6, 2, 5, 1};
        System.out.println(new Solution64().maxInWindows(nums, 3));
    }

    public ArrayList<Integer> maxInWindows(int[] num, int size) {
        ArrayList<Integer> results = new ArrayList<>();
        if (num == null || num.length == 0 || num.length < size || size <= 0) {
            return results;
        }
        LinkedList<Integer> integers = new LinkedList<>();
        for (int i = 0; i < num.length; i++) {
            while (!integers.isEmpty() && num[integers.peekLast()] < num[i]) {
                integers.removeLast();
            }
            integers.addLast(i);
            while (i - integers.peekFirst() >= size) {
                integers.removeFirst();
            }
            if (i >= size - 1) {
                results.add(num[integers.peekFirst()]);
            }
        }
        return results;
    }
}

C++ 代码如下：

class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size) {
        vector<int> results ;
        if (num.size() == 0 || num.size() < size || size <= 0) {
            return results;
        }
        deque<int> integers;
        for (int i = 0; i < num.size(); i++) {
            while (integers.size()>0 && num[integers.back()] < num[i]) {
                integers.pop_back();
            }
            integers.push_back(i);
            while (i - integers.front() >= size) {
                integers.pop_front();
            }
            if (i >= size - 1) {
                results.push_back(num[integers.front()]);
            }
        }
        return results;
    }
};

时间复杂度：O（n）,所有的元素都进入队列，再出队列 空间复杂度：O(n)，使用额外的队列空间存储索引以及窗口最大值。