题目描述

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。 例如矩阵：

中包含一条字符串 "bcced" 的路径，但是矩阵中不包含 "abcb" 路径，因为字符串的第一个字符 b 占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

示例1

输入

 [[a,b,c,e],[s,f,c,s],[a,d,e,e]],"abcced"

返回值

true

思路 & 解答

主要的思路是对于每一个字符为起点，递归向四周拓展，然后遇到不匹配返回 false ，匹配则接着匹配直到完成，里面包含了 回溯 的思想。步骤如下：

针对每一个字符为起点，初始化一个和矩阵一样大小的标识数组，标识该位置是否被访问过，一开始默认是false。

1. 如果当前的字符索引已经超过了字符串长度，说明前面已经完全匹配成功，直接返回 true
2. 如果行索引和列索引，不在有效的范围内，或者改位置已经标识被访问，直接返回 false
3. 否则将当前标识置为已经访问过
4. 如果矩阵当前位置的字符和字符串相等，那么就字符串的索引加一，递归判断周边的四个，只要一个的结果为 true，就返回 true，否则将该位置置为没有访问过（相当于回溯，退回上一步），返回 false。矩阵当前位置的字符和字符串不相等，否则同样也是将该位置置为没有访问过（相当于回溯，退回上一步），返回 false。

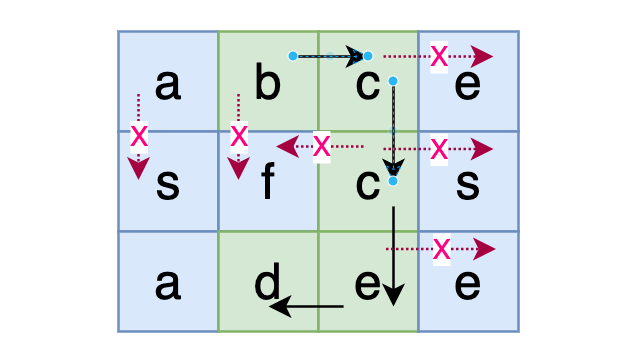
比如查找 bcced:

import java.util.*;

public class Solution {
    public boolean hasPath(char[][] matrix, String word) {
        // write code here
        if (matrix == null || word == null || word.length() == 0) {
            return false;
        }
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                boolean[][] flags = new boolean[matrix.length][matrix[0].length];
                boolean result = judge(i, j, matrix, flags, word, 0);
                if (result) {
                    return true;
                }
            }
        }
        return false;
    }

    public boolean judge(int i, int j, char[][] matrix, boolean[][] flags, String words, int index) {
        if (index >= words.length()) {
            return true;
        }
        if (i < 0 || j < 0 || i >= matrix.length || j >= matrix[0].length || flags[i][j]) {
            return false;
        }
        flags[i][j] = true;
        if (matrix[i][j] == words.charAt(index)) {
            if (judge(i - 1, j, matrix, flags, words, index + 1)
                    || judge(i + 1, j, matrix, flags, words, index + 1)
                    || judge(i, j + 1, matrix, flags, words, index + 1)
                    || judge(i, j - 1, matrix, flags, words, index + 1)) {
                return true;
            } else {
                flags[i][j] = false;
                return false;
            }
        } else {
            flags[i][j] = false;
            return false;
        }
    }
}

C++ 代码如下：

#include <iostream>
#include <vector>

using namespace std;

class Solution {
public:
    bool hasPath(vector<vector<char> >& matrix, string word) {
        if ( word.length() == 0) {
            return false;
        }
        vector<vector<bool> > flags(matrix.size(),vector<bool>(matrix[0].size(),0));
        for (int i = 0; i < matrix.size(); i++) {
            for (int j = 0; j < matrix[0].size(); j++) {
                bool result = judge(i, j, matrix, flags, word, 0);
                if (result) {
                    return true;
                }
            }
        }
        return false;
    }
    bool judge(int i, int j, vector<vector<char> >& matrix, vector<vector<bool> >& flags, string& words, int index) {
        if (index >= words.length()) {
            return true;
        }
        if (i < 0 || j < 0 || i >= matrix.size() || j >= matrix[0].size() || flags[i][j]) {
            return false;
        }
        flags[i][j] = true;
        if (matrix[i][j] == words[index]) {
            if (judge(i - 1, j, matrix, flags, words, index + 1)
                || judge(i + 1, j, matrix, flags, words, index + 1)
                || judge(i, j + 1, matrix, flags, words, index + 1)
                || judge(i, j - 1, matrix, flags, words, index + 1)) {
                return true;
            } else {
                flags[i][j] = false;
                return false;
            }
        } else {
            flags[i][j] = false;
            return false;
        }
    }
};

时间复杂度: 最坏的情况是将棋盘的每个位置都遍历一次，而每个位置除首字母外都不能走已经走过的位置，故四个方向只有三个方向可以选择，故时间复杂度为 O(mn*k³), m * n是矩阵大小。 空间复杂度: 借助了额外的空间表示是否被访问过，空间复杂度为 O(m * n)。

其实也有一种做法是直接在原来的矩阵上用特殊的字符表示已经访问过，而不需要额外的矩阵空间，这样空间复杂度更小，这里不再演示。