题目描述
统计一个数字在升序数组中出现的次数。
示例1
输入
[1,2,3,3,3,3,4,5],3
返回值
4
思路 & 解答
如果使用暴力法,可以直接统计,但是明显这不是我们希望得到的解法。
由于数组是有序的,可以明显看到是分治法。
第1步是找出数值为k的数的索引:
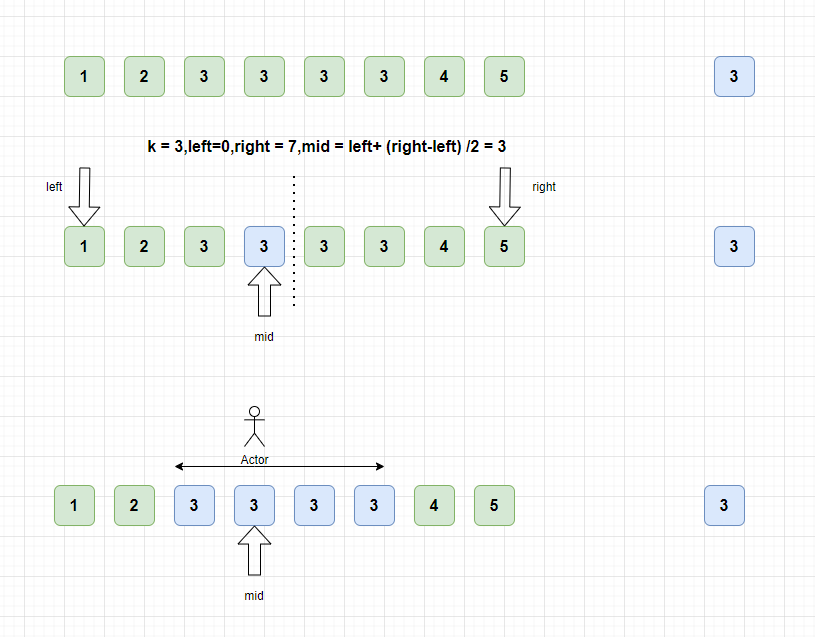
假设数组为nums[],一开始的左边索引为left = 0,右边界索引为right = nums.length-1
-
- 将数组分成两部分,中间的数为
nums[mid]。第1部分为[left,mid],第2部分为[mid+1,right]。
- 将数组分成两部分,中间的数为
-
- 如果
nums[mid]>k,则说明 k 只可能存在前半部分中,对前半部分执行操作1。
- 如果
-
- 如果
nums[mid]<k,则说明 k 只可能存在后半部分中,对后半部分执行操作1。
- 如果
-
- 如果
nums[mid]=k,直接返回当前索引mid。
- 如果
-
- 如果
left > right,说明 k 不存在,则返回-1。
- 如果
找到索引之后,往两边扩展,同时统计k的个数,直到元素不等于k的时候停止。
代码如下:
public class Solution53 {
public static void main(String[] args) {
Solution37 solution37 = new Solution37();
int[] nums = new int[]{1, 2, 3, 3, 3, 3, 4, 5};
solution37.GetNumberOfK(nums, 3);
}
public int GetNumberOfK(int[] array, int k) {
// 数组为空或者数组元素个数为0,直接返回
if (array == null || array.length == 0) {
return 0;
}
// 使用二分法,找出等于k的数的索引
int index = findIndex(array, k, 0, array.length - 1);
// 索引为-1,则说明该数不存在
if (index == -1) {
return 0;
}
// 存在则index处存在一个
int count = 1;
// 向左边拓展,计算相等的个数
for (int left = index - 1; left >= 0; left--) {
if (array[left] == k) {
count++;
}
}
// 向右边拓展,计算相等的个数
for (int right = index + 1; right < array.length; right++) {
if (array[right] == k) {
count++;
}
}
return count;
}
public int findIndex(int[] array, int k, int left, int right) {
// 只剩下一个数,直接和k比较
if (left == right) {
return array[left] == k ? left : -1;
} else {
// 中间的数索引为mid。将数组分为两半
int mid = left + (right - left) / 2;
// 等于k直接返回当前索引
if (array[mid] == k) {
return mid;
} else if (array[mid] < k) {
// mid索引的数小于k,则k只可能在右边一半
return findIndex(array, k, mid + 1, right);
} else {
// 否则在左边一半
return findIndex(array, k, left, mid - 1);
}
}
}
}
C++ 代码如下:
class Solution {
public:
int GetNumberOfK(vector<int> array ,int k) {
// 数组为空或者数组元素个数为0,直接返回
if ( array.size() == 0) {
return 0;
}
// 使用二分法,找出等于k的数的索引
int index = findIndex(array, k, 0, array.size() - 1);
// 索引为-1,则说明该数不存在
if (index == -1) {
return 0;
}
// 存在则index处存在一个
int count = 1;
// 向左边拓展,计算相等的个数
for (int left = index - 1; left >= 0; left--) {
if (array[left] == k) {
count++;
}
}
// 向右边拓展,计算相等的个数
for (int right = index + 1; right < array.size(); right++) {
if (array[right] == k) {
count++;
}
}
return count;
}
int findIndex(vector<int> array, int k, int left, int right) {
// 只剩下一个数,直接和k比较
if (left == right) {
return array[left] == k ? left : -1;
} else {
// 中间的数索引为mid。将数组分为两半
int mid = left + (right - left) / 2;
// 等于k直接返回当前索引
if (array[mid] == k) {
return mid;
} else if (array[mid] < k) {
// mid索引的数小于k,则k只可能在右边一半
return findIndex(array, k, mid + 1, right);
} else {
// 否则在左边一半
return findIndex(array, k, left, mid - 1);
}
}
}
};
时间复杂度:O(logn)
空间复杂度:O(1)
