题目描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

示例1 输入

{1,2,3,4,5,#,6,#,#,7}

返回值

4

思路 & 解答

声明：这里的输入是一个数的根节点，也就是从根节点，我们就可以获取到树的所有节点，而类似数组的表达方式{1,2,3,4,5,#,6,#,#,7}，则是按照层次来放的。(比如这个树就是4层)

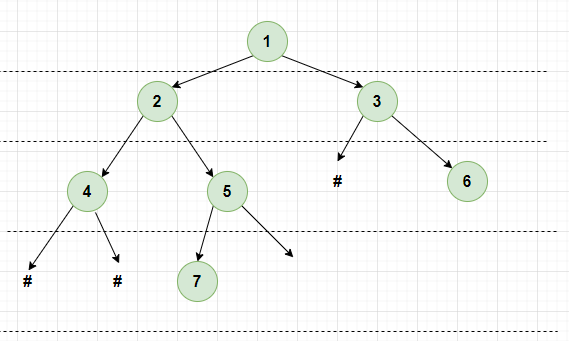
递归左右子树

第一种方法比较容易想到，对于任意一个节点node而言，我要想知道当前node节点（包括当前节点）的深度，肯定得求当前节点的左边节点（设为left）的深度leftDeepth，以及获取右节点（设为right）的深度rightDeepth，然后求两者最大+1（Max{leftDeepth,rightDeepth}+1），就是当前节点的深度。

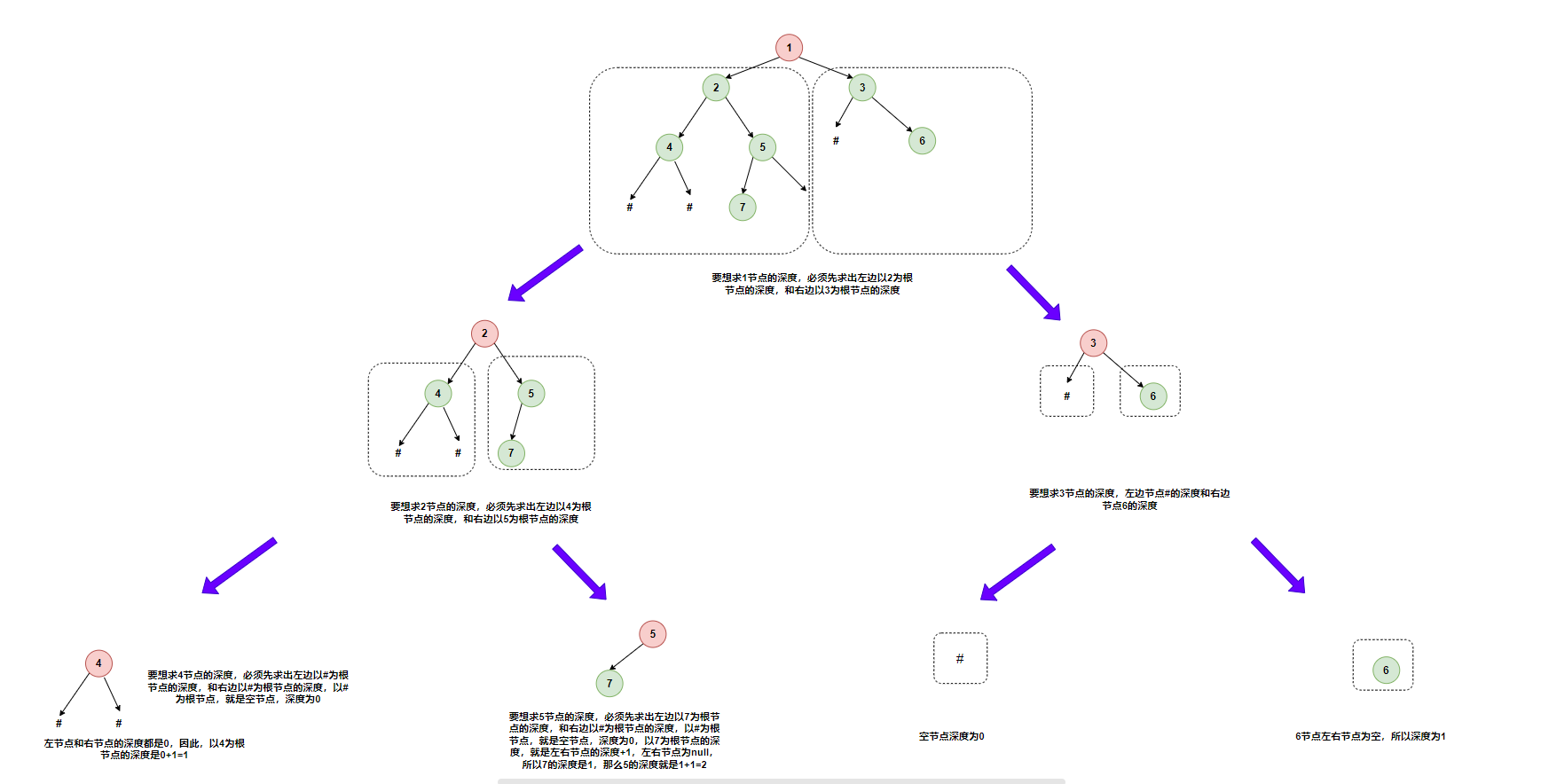
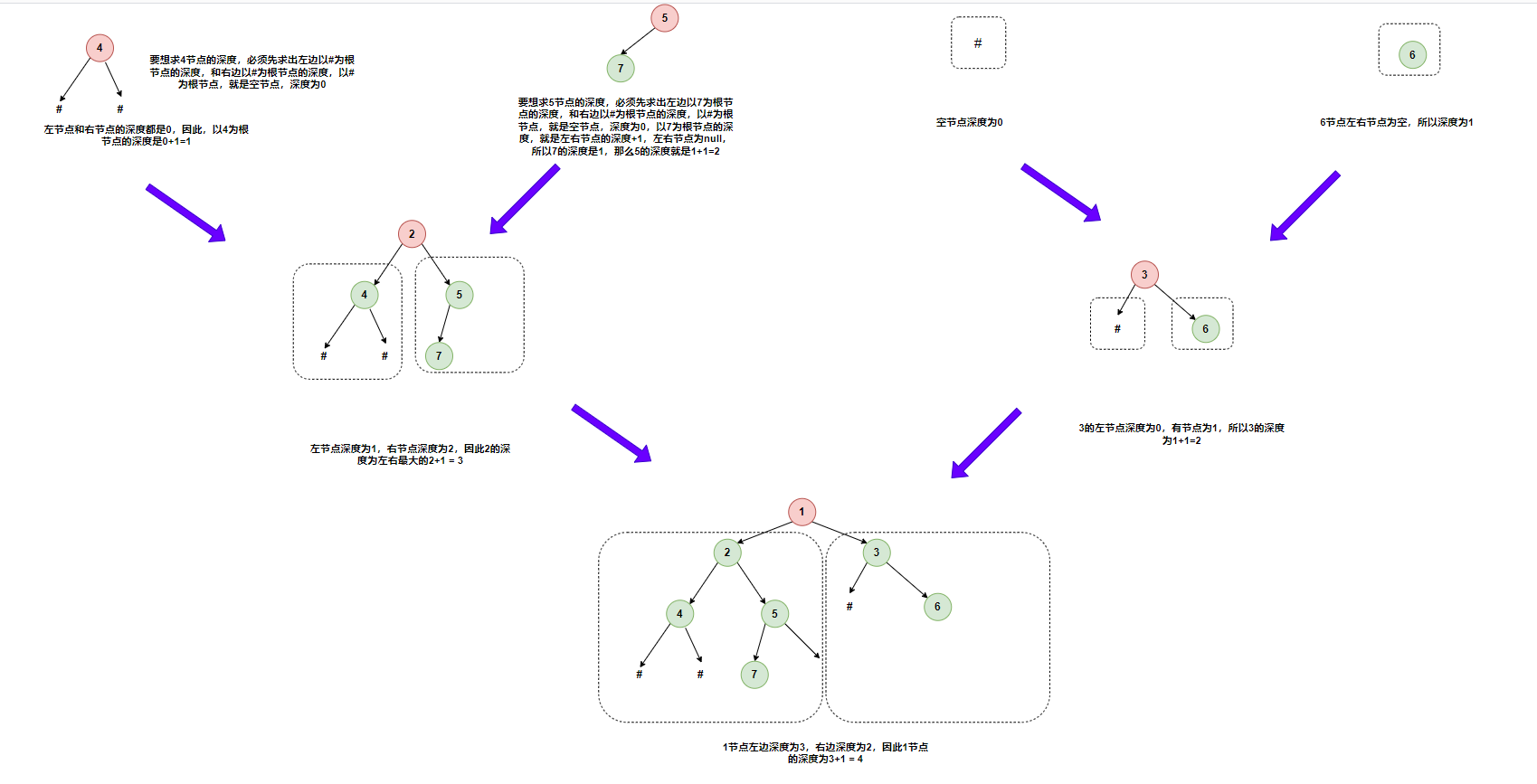
而递归中比较重要的一点，是结束条件。在这道题中，如果一个节点为null，就结束，并且当前节点的深度是0。代码超级无敌短：

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root==null)
            return 0;
        return Math.max(TreeDepth(root.left),TreeDepth(root.right))+1;
    }
}

C++ 代码如下：

class Solution {
public:
    int TreeDepth(TreeNode *root) {
        if (root == NULL)
            return 0;
        return max(TreeDepth(root->left), TreeDepth(root->right)) + 1;
    }
};

使用队列层次计算深度

这是同事@小陈同学提出的做法，思路是如果树的根节点不为空，则将根节点放进队列中。 设置深度deep为0。 使用while循环，只要队列不为空，则执行下面操作： 1.获取队列的大小size。 2.依次取出队列的前size个元素，如果该元素的左边节点不为空，则将左边节点放进队列，如果该元素的右边节点不为空，则将该元素的右边节点放进队列。 3. 层次deep+1

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
import java.util.LinkedList;
import java.util.Queue;
public class Solution {
    public int TreeDepth(TreeNode root) {
      Queue<TreeNode> tree = new LinkedList<>();
        if (root != null) {
            tree.add(root);
        }
        int length = 0;
        while (!tree.isEmpty()) {
            int size = tree.size();
            while (size > 0) {
                TreeNode node = tree.peek();
                if (node.left != null) {
                    tree.add(node.left);
                }
                if (node.right != null) {
                    tree.add(node.right);
                }
                tree.remove(node);
                size--;
            }
            length++;
        }
        return length;  
    }
}

C++ 代码实现如下：

class Solution {
public:
    int TreeDepth(TreeNode *root) {
        deque<TreeNode *> tree;
        if (root != NULL) {
            tree.push_back(root);
        }
        int length = 0;
        while (tree.size() > 0) {
            int size = tree.size();
            while (size > 0) {
                TreeNode *node = tree.front();
                if (node->left != NULL) {
                    tree.push_back(node->left);
                }
                if (node->right != NULL) {
                    tree.push_back(node->right);
                }
                tree.pop_front();
                size--;
            }
            length++;
        }
        return length;
    }
};

• 时间复杂度为：O(n)，所有的节点需要进入队列，再出队列
• 空间复杂度：O(n),借助了额外的队列空间。