题目描述
给定一个二叉树root和一个值 sum ,判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
- 1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
- 2.叶子节点是指没有子节点的节点
- 3.路径只能从父节点到子节点,不能从子节点到父节点
- 4.总节点数目为n
例如: 给出如下的二叉树,sum=22:
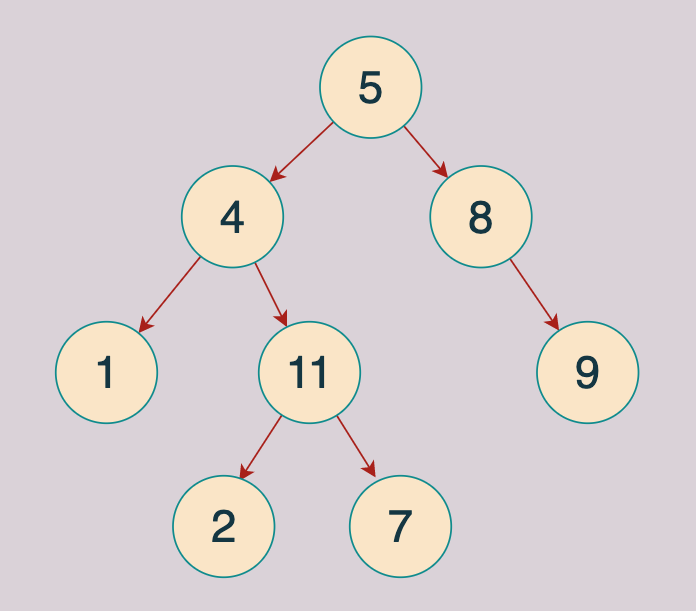
返回true,因为存在一条路径 5 -> 4 -> 11 -> 2 的节点值之和为 22
思路 & 解答
前面其实我们有做过这道题,而且需要保存路径,因此需要使用队列,,将遍历的节点放进队列中,到叶子节点之后计算和,然后再回溯到上面一层的时候,将队列最后一个元素取出来(这个时候需要将和加回来),放进当前的元素。
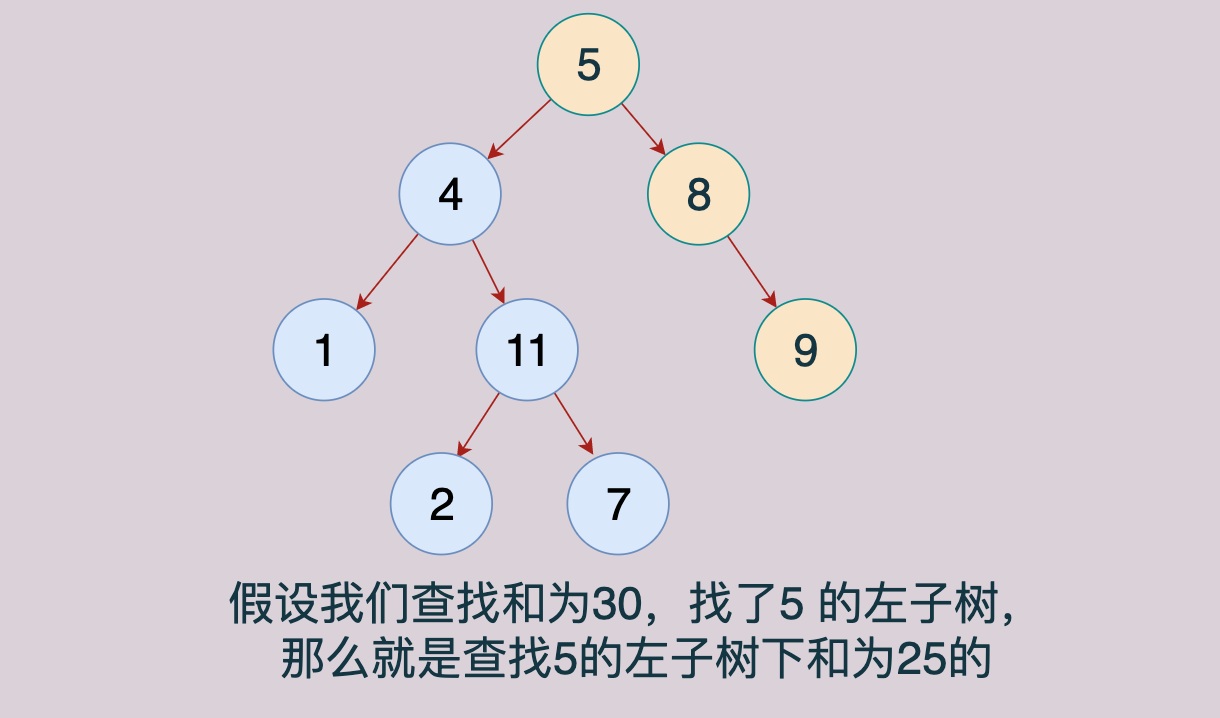
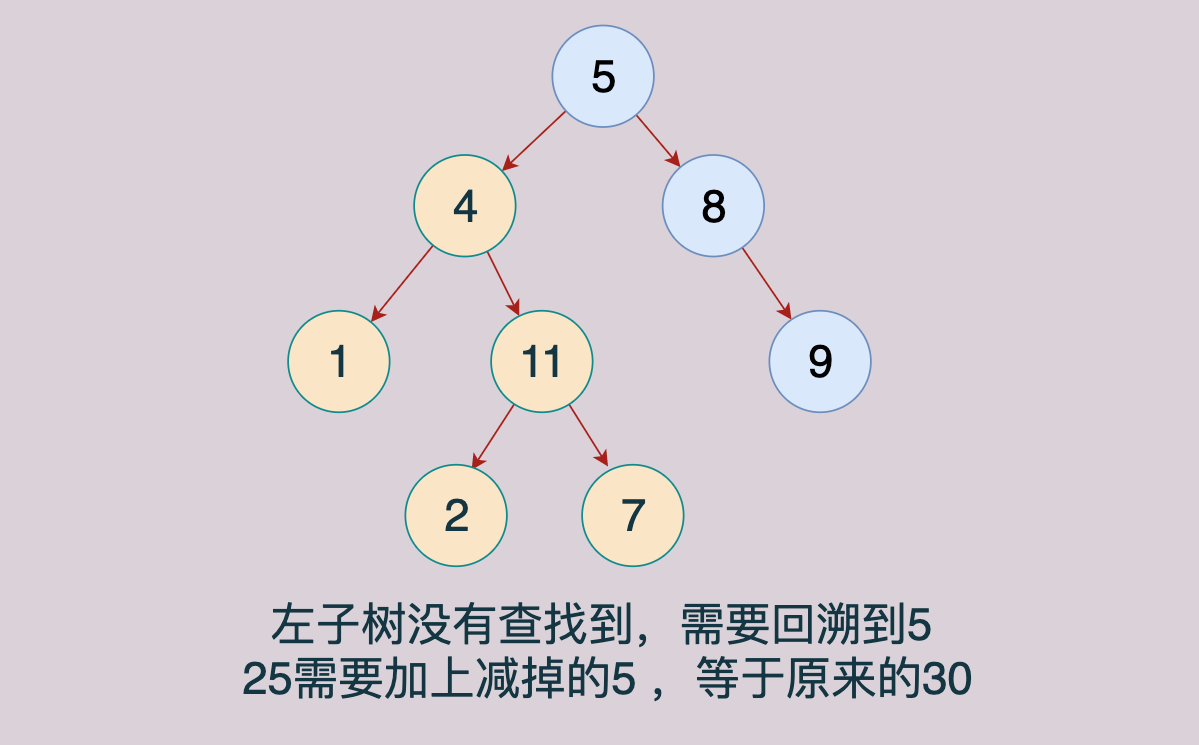
代码如下:
import java.util.ArrayList;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.stream.Collectors;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ArrayList<ArrayList<Integer>> FindPath(TreeNode root, int target) {
ArrayList<ArrayList<Integer>> results = new ArrayList<>();
LinkedList<Integer> queue = new LinkedList<>();
int sum = 0;
if (root != null) {
addDatas(root, target, results, queue, sum);
}
return results;
}
public void addDatas(TreeNode root, int target, ArrayList<ArrayList<Integer>> results, LinkedList<Integer> queue, Integer sum) {
if (root != null) {
sum = sum + root.val;
queue.add(root.val);
if (sum == target && root.left == null && root.right == null) {
addResult(results, queue);
} else {
addDatas(root.left, target, results, queue, sum);
addDatas(root.right, target, results, queue, sum);
}
queue.pollLast();
sum = sum - root.val;
}
}
public void addResult(ArrayList<ArrayList<Integer>> results, Queue<Integer> queue) {
ArrayList<Integer> result = (ArrayList<Integer>) queue.stream().collect(Collectors.toList());
results.add(result);
}
}
C++ 代码如下:
class Solution {
public:
vector<vector<int>> FindPath(TreeNode* root, int target) {
vector<vector<int>> results;
deque<int> queue;
int sum = 0;
if (root != NULL) {
addDatas(root, target, results, queue, sum);
}
return results;
}
void addDatas(TreeNode* root, int target, vector<vector<int>>& results, deque<int>& queue, int sum) {
if (root != NULL) {
sum = sum + root->val;
queue.push_back(root->val);
if (sum == target && root->left == NULL && root->right == NULL) {
addResult(results, queue);
} else {
addDatas(root->left, target, results, queue, sum);
addDatas(root->right, target, results, queue, sum);
}
queue.pop_back();
sum = sum - root->val;
}
}
void addResult(vector<vector<int>>& results, deque<int>& queue) {
vector<int> result;
for(int i:queue){
result.push_back(i);
}
results.push_back(result);
}
};
这道题由于不需要保存路径,直接递归的时候不断减去当前节点的值就可以,直到叶子节点,如果为0,那么说明这条路径符合,只要知道任何一条符合即可返回,不需要遍历所有的路径。
Java 代码实现如下:
public class Solution82 {
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) {
return false;
}
return dfs(root, sum);
}
private boolean dfs(TreeNode curNode, int target) {
if (curNode == null) {
return false;
}
target = target - curNode.val;
// 叶子节点并且target减到0,说明符合
if (curNode.left == null && curNode.right == null && target == 0) {
return true;
}
// 递归左右子树
return dfs(curNode.left, target) || dfs(curNode.right, target);
}
}
C++ 代码如下:
class Solution {
public:
bool hasPathSum(TreeNode *root, int sum) {
if (root == NULL) {
return false;
}
return dfs(root, sum);
}
bool dfs(TreeNode *curNode, int target) {
if (curNode == NULL) {
return false;
}
target = target - curNode->val;
// 叶子节点并且target减到0,说明符合
if (curNode->left == NULL && curNode->right == NULL && target == 0) {
return true;
}
// 递归左右子树
return dfs(curNode->left, target) || dfs(curNode->right, target);
}
};
- 时间复杂度 O(n) : n 为二叉树的节点数,最差遍历所有节点
- 空间复杂度 O(1) :没有使用额外空间
