题目描述

请实现一个函数，用来判断一棵二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

例如：下面这棵二叉树是对称的

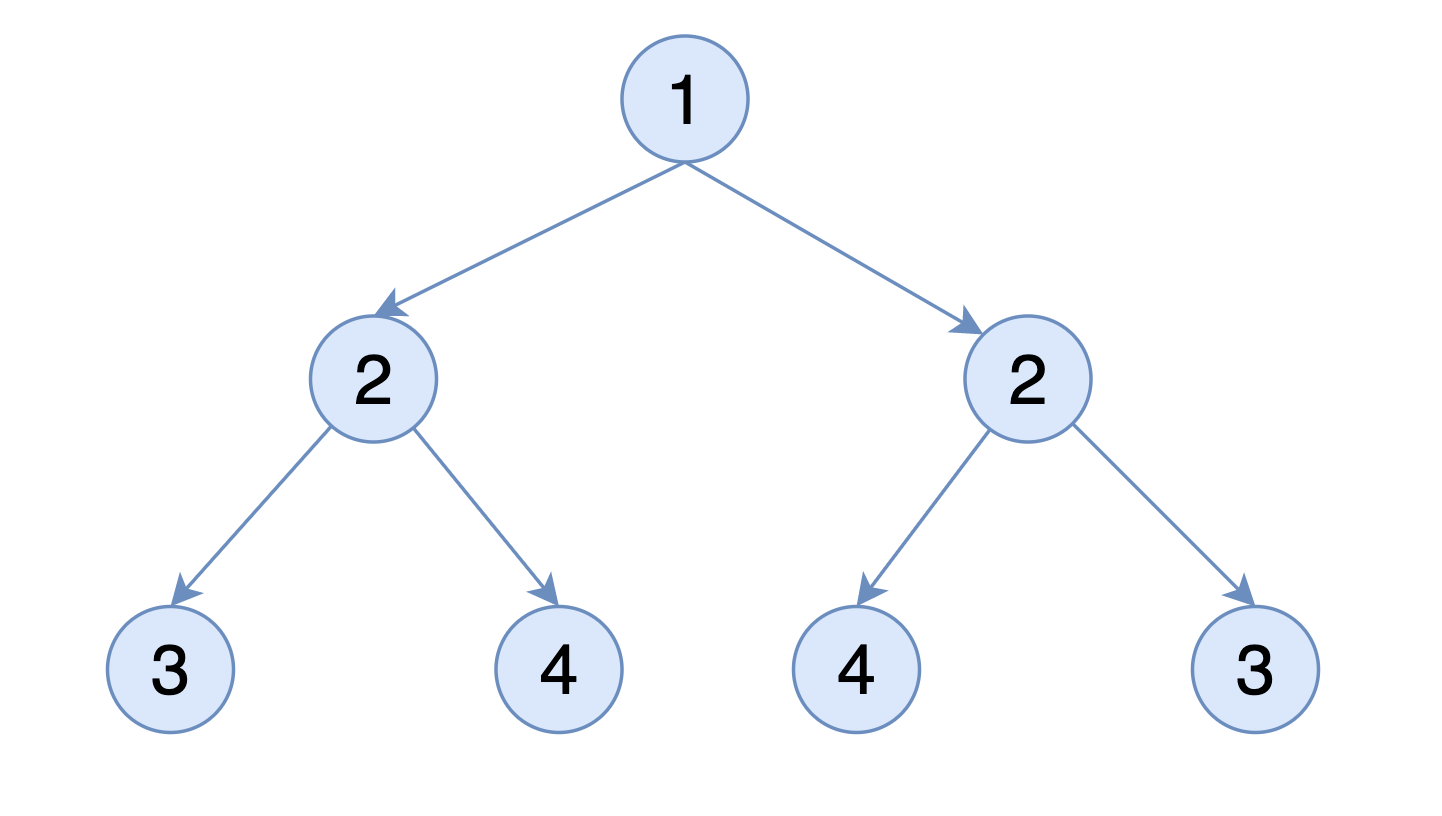
下面这个就不是对称的：

示例1

输入

{8,6,6,5,7,7,5}

返回值

true

示例2

输入

{8,6,9,5,7,7,5}

返回值

false

思路 & 解答

主要是使用递归，先判断根节点是否为空，不为空则判断左右子树是不是对称。

如果左右子树都为空，则返回 true，如果有一个为空，则返回 false，如果两个都不为空的时候，除了对比左右两个节点的值，还需要递归，对比左子树的左子树和右子树的右子树是否相等，左子树的右子树和右子树的左子树是否相等。

Java 代码如下：

public class Solution28 {
    public boolean jude(TreeNode left, TreeNode right) {
        // 如果左右两个都为空，则对称
        if (left == null && right == null) {
            return true;
        } else if (left == null || right == null) {
            // 如果左右两个有一个为空，那么就不对称
            return false;
        }
        // 都不为空的情况，需要判断两个的值，是不是相等
        if (left.val != right.val) {
            return false;
        } else {
            // 递归判断，左子树的左子树和右子树的右子树，左子树的右子树和右子树的左子树
            return jude(left.left, right.right) && jude(left.right, right.left);
        }
    }

    public boolean isSymmetrical(TreeNode pRoot) {
        // 判断根节点是否为空，如果不为空则判断左右子树
        return pRoot==null || jude(pRoot.left, pRoot.right);
    }
}

C++ 代码如下：

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    bool isSymmetrical(TreeNode *pRoot) {
        // 判断根节点是否为空，如果不为空则判断左右子树
        return pRoot == NULL || jude(pRoot->left, pRoot->right);
    }

    bool jude(TreeNode *left, TreeNode *right) {
        // 如果左右两个都为空，则对称
        if (left == NULL && right == NULL) {
            return true;
        } else if (left == NULL || right == NULL) {
            // 如果左右两个有一个为空，那么就不对称
            return false;
        }
        // 都不为空的情况，需要判断两个的值，是不是相等
        if (left->val != right->val) {
            return false;
        } else {
            // 递归判断，左子树的左子树和右子树的右子树，左子树的右子树和右子树的左子树
            return jude(left->left, right->right) && jude(left->right, right->left);
        }
    }

};

时间复杂度：O(n) 空间复杂度：O(n),最坏情况下，二叉树退化为链表

另外一种，非递归的做法，是借助两个队列，按照层次，一个是按照从左到右添加元素，另外一个队列是按照从右到左添加元素，挨个取出来，进行对比，不等则说明不对称，如果相等，则再把其左右子树分别按照不同的顺序添加到队列中。代码如下：

import java.util.LinkedList;

public class Solution {
    boolean isSymmetrical(TreeNode pRoot)
    {
        if (pRoot == null)
            return true;
        LinkedList<TreeNode> leftNodes = new LinkedList<>();
        LinkedList<TreeNode> rightNodes = new LinkedList<>();
        leftNodes.add(pRoot.left);
        rightNodes.add(pRoot.right);
        while (!leftNodes.isEmpty() && !rightNodes.isEmpty()) {
            TreeNode leftNode = leftNodes.poll();
            TreeNode rightNode = rightNodes.poll();
            if (leftNode == null && rightNode == null)
                continue;
            if (leftNode == null || rightNode == null)
                return false;
            // 取出来对比
            if (leftNode.val != rightNode.val)
                return false;
            // 从左往右添加节点
            leftNodes.add(leftNode.left);
            leftNodes.add(leftNode.right);
            // 从右往左添加节点
            rightNodes.add(rightNode.right);
            rightNodes.add(rightNode.left);
        }
        return leftNodes.isEmpty() && rightNodes.isEmpty();
    }
}

C++ 代码如下：

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    bool isSymmetrical(TreeNode *pRoot) {
        if (pRoot == NULL)
            return true;
        deque<TreeNode *> leftNodes;
        deque<TreeNode *> rightNodes;
        leftNodes.push_back(pRoot->left);
        rightNodes.push_back(pRoot->right);
        while (leftNodes.size() != 0 && rightNodes.size() > 0) {
            TreeNode *leftNode = leftNodes.front();
            leftNodes.pop_front();
            TreeNode *rightNode = rightNodes.front();
            rightNodes.pop_front();
            if (leftNode == NULL && rightNode == NULL)
                continue;
            if (leftNode == NULL || rightNode == NULL)
                return false;
            // 取出来对比
            if (leftNode->val != rightNode->val)
                return false;
            // 从左往右添加节点
            leftNodes.push_back(leftNode->left);
            leftNodes.push_back(leftNode->right);
            // 从右往左添加节点
            rightNodes.push_back(rightNode->right);
            rightNodes.push_back(rightNode->left);
        }
        return leftNodes.size() == 0 && rightNodes.size() == 0;
    }

};

空间复杂度为 O(n)，时间复杂度为 O(n),每个节点只会入队出队一次。