题目描述

给定一个二叉树root和一个整数值 sum ，求该树有多少路径的的节点值之和等于 sum 。

• 1.该题路径定义不需要从根节点开始，也不需要在叶子节点结束，但是一定是从父亲节点往下到孩子节点
• 2.总节点数目为 n
• 3.保证最后返回的路径个数在整形范围内

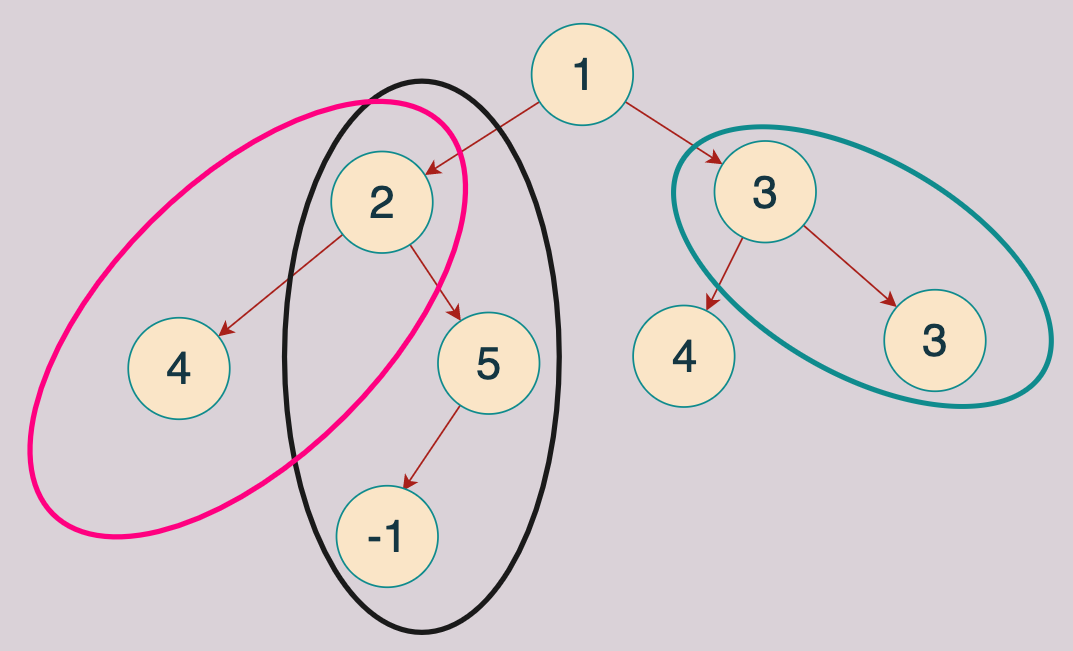
假如二叉树 root为 {1,2,3,4,5,4,3,#,#,-1}，sum=6，那么总共如下所示，

思路 & 解答

这道题值得注意的是，开始不一定在根节点，结束也不一定在叶子节点，因此每个节点都可以往下递归查找的。

每次查找到一个节点的时候，用 sum 减去当前节点的值，如果等于 0，就说明前面的节点到当前节点满足和为 sum，此时注意不要 return，因为下面还需要继续查找，比如存在-1 和 1 的路径，加起来还是会满足的。

如果不想在递归中来回传递变量，可以使用一个全局变量来保存结果：

public class Solution84 {
    public int sum = 0;

    public void dfs(TreeNode root, int sum) {
        if (null == root) return;
        sum -= root.val;
        if (sum == 0) {
            this.sum++;
        }
        dfs(root.left, sum);
        dfs(root.right, sum);
    }

    public int FindPath(TreeNode root, int sum) {
        if (null == root) return this.sum;
        // 当前节点往下遍历
        dfs(root, sum);
        // 在左子树查找（不包括当前节点）
        FindPath(root.left, sum);
        // 在右子树查找（不包括当前节点）
        FindPath(root.right, sum);
        return this.sum;
    }
}

C++ 代码如下：

class Solution {
public:
    int sum = 0;

    int FindPath(TreeNode *root, int sum) {
        if (NULL == root) return this->sum;
        // 当前节点往下遍历
        dfs(root, sum);
        // 在左子树查找（不包括当前节点）
        FindPath(root->left, sum);
        // 在右子树查找（不包括当前节点）
        FindPath(root->right, sum);
        return this->sum;
    }

    void dfs(TreeNode *root, int sum) {
        if (NULL == root) return;
        sum -= root->val;
        if (sum == 0) {
            this->sum++;
        }
        dfs(root->left, sum);
        dfs(root->right, sum);
    }
};