题目描述
输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。
在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树
平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
样例解释:

样例二叉树如图,为一颗平衡二叉树
注:我们约定空树是平衡二叉树。
- 输入描述:输入一棵二叉树的根节点
- 返回值描述:输出一个布尔类型的值
示例 1
输入: {1,2,3,4,5,6,7}
输出: true
示例 2
输入: {}
输出: true
思路 & 解答
平衡树意味着我们需要对比任何在同一个根下的左右子树的高度差,还记得之前我们计算树的高度么,使用递归方式来解决,其实这道题与算高度差不多,只是两边高度需要算出一个差值。
算法的主要思想:
- 不断对比每两个节点的左右子树的最大高度差,注意取差的绝对值,需要小于等于1
- 对比完左右子树之后,需要递归左子树以及右子树进行分别判断,都满足才是平衡树
Java 代码如下:
public class Solution79 {
public boolean IsBalanced_Solution(TreeNode root) {
if (root == null) return true;
// 当前左右子树是否平衡以及左右子树分别是否平衡
return Math.abs(depth(root.left) - depth(root.right)) <= 1 && IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);
}
private int depth(TreeNode root) {
if (root == null) {
return 0;
}
// 递归获取深度
return Math.max(depth(root.left), depth(root.right)) + 1;
}
}
C++ 代码如下:
class Solution {
public:
bool IsBalanced_Solution(TreeNode* root) {
if (root == NULL) return true;
// 当前左右子树是否平衡以及左右子树分别是否平衡
return abs(depth(root->left) - depth(root->right)) <= 1
&& IsBalanced_Solution(root->left) && IsBalanced_Solution(root->right);
}
int depth(TreeNode* root) {
if (root == NULL) {
return 0;
}
// 递归获取深度
return max(depth(root->left), depth(root->right)) + 1;
}
};
- 时间复杂度
O(nlogn):最差情况下,需要遍历树所有节点判断是否平衡,需要O(n)。但是判断每个节点最大高度需要递归左右子树,需要占用O(log2n),所以总共占用O(Nlog2n) - 空间复杂度
O(n):最差情况下,也就是树退化为链表时,递归需要使用O(n)的栈空间,严格意义上递归栈也需要空间。
但是上面的计算,仔细观察就会发现会有很多重复计算的过程,比如下面的数,计算子树深度的时候,计算 1 的左子树,和计算 2 的,基本都重复了。
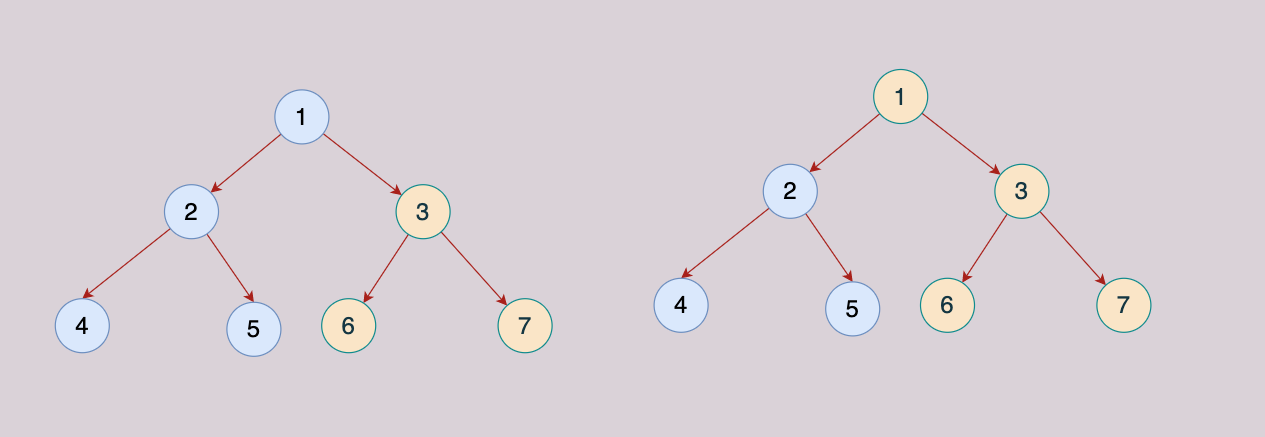
应该如何避免这种重复计算呢?前面的是自顶向下的方式,因为每个节点都得把子树计算一遍才需要重复,如果我们从下往上计算,那不就避免了重复计算,对比逻辑如下:
- 如果当前节点为空,高度为0
- 如果当前节点的左子树的高度为-1,那么说明不平衡,否则,需要计算右子树高度,同样需要不等于-1,如果两者的差不符合小于等于1,那么说明它们不平衡,返回-1。通过这样 -1 异常值就会一路返回,到最初的调用处,得到不平衡的结果。
Java 代码如下:
public class Solution79 {
public boolean IsBalanced_Solution(TreeNode root) {
// 空树
if (root == null) {
return true;
}
return getHeight(root) != -1;
}
public int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
// 左子树的高度
int left = getHeight(root.left);
if (left < 0) {
return -1;
}
// 右子树的高度
int right = getHeight(root.right);
if (right < 0) {
return -1;
}
return Math.abs(left - right) > 1 ? -1 : 1 + Math.max(left, right);
}
}
C++ 代码如下:
class Solution {
public:
bool IsBalanced_Solution(TreeNode* root) {
// 空树
if (root == NULL) {
return true;
}
return getHeight(root) != -1;
}
int getHeight(TreeNode* root) {
if (root == NULL) {
return 0;
}
// 左子树的高度
int left = getHeight(root->left);
if (left < 0) {
return -1;
}
// 右子树的高度
int right = getHeight(root->right);
if (right < 0) {
return -1;
}
return abs(left - right) > 1 ? -1 : 1 + max(left, right);
}
};
- 时间复杂度
O(n):每个节点计算一次 - 空间复杂度
O(n):递归需要使用额外堆栈空间
