题目描述

假设你有一个数组prices，长度为n，其中prices[i]是股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

• 1.你可以买入一次股票和卖出一次股票，并非每天都可以买入或卖出一次，总共只能买入和卖出一次，且买入必须在卖出的前面的某一天
• 2.如果不能获取到任何利润，请返回0
• 3.假设买入卖出均无手续费

示例1

输入：[8,9,2,5,4,7,1]

返回值: 5

说明: 在第3天(股票价格 = 2)的时候买入，在第6天(股票价格 = 7)的时候卖出，最大利润 = 7-2 = 5 ，不能选择在第2天买入，第3天卖出，这样就亏损7了；同时，你也不能在买入前卖出股票。

示例2

输入：[2,4,1]

返回值: 2

思路 & 解答

暴力穷举

这里涉及的节点无非是买入，卖出，那么我们遍历所有的数据，作为买入日期，同时将该日期后面每一个都作为卖出日期来计算，只要维护最大的利润即可。

Java 代码如下：

public class Solution63 {
    public int maxProfit(int[] prices) {
        int ans = 0;
        int len = prices.length;
        // 买入时间
        for (int i = 0; i < len; i++) {
            // 卖出时间
            for (int j = 0; j < i; j++) {
                // 最大的收益
                ans = Math.max(ans, prices[i] - prices[j]);
            }
        }
        return ans;
    }
}

C++ 代码如下：

class Solution {
public:
    int maxProfit(vector<int> &prices) {
        int result = 0;
        int len = prices.size();
        // 买入时间
        for (int i = 0; i < len; i++) {
            // 卖出时间
            for (int j = 0; j < i; j++) {
                // 最大的收益
                result = max(result, prices[i] - prices[j]);
            }
        }
        return result;
    }
};

• 时间复杂度： O(n²)
• 空间复杂度：O(1)

贪心法

我们要想得到一个最大的利润，其实就是要两者差值最大。如果让差值最大，假设在当天卖出，那么什么时候买入最好呢？

当然是在前面找到最小的买入点，比如：

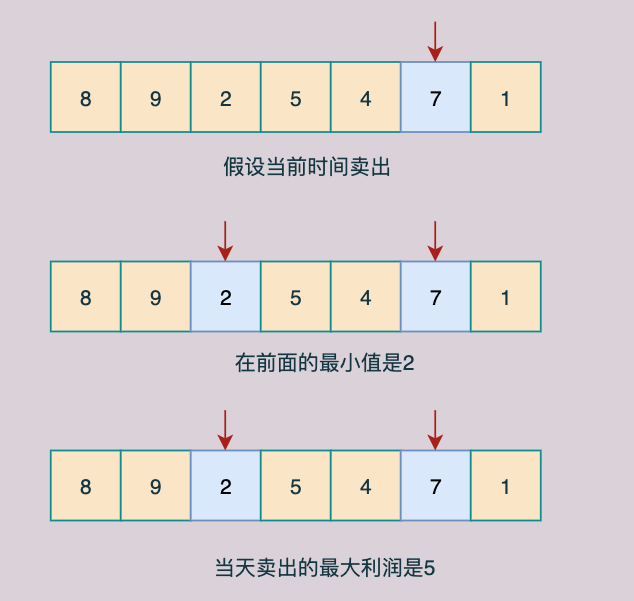
而前面的最小值，其实我们在遍历的时候是可以不断维护的，所以我们只要遍历一次数组即可。

Java 代码如下：

public class Solution63 {
    public int maxProfit(int[] prices) {
        int min = Integer.MAX_VALUE;
        int result = 0;
        for (int value : prices) {
            // 维护最小值
            min = Math.min(min, value);
            // 当前值减去前面最小值，与利润最大值对比，维护好利润最大值
            result = Math.max(result, value - min);
        }
        return result;
    }
}

C++ 代码如下：

class Solution {
public:
    int maxProfit(vector<int> &prices) {
        int minValue = INT_MAX;
        int result = 0;
        for (int value : prices) {
            // 维护最小值
            minValue = min(minValue, value);
            // 当前值减去前面最小值，与利润最大值对比，维护好利润最大值
            result = max(result, value - minValue);
        }
        return result;
    }
};

时间复杂度为O(n),空间复杂度为O(1)

其实还有单调栈的写法，也就是栈顶的元素永远是前面遍历的元素里面最小的，这样我们每次都是和栈顶元素相减，这个和上面的贪心算法其实是一样的，只不过上面的用min来存储最小值，单调栈用栈来保存。